Difference between revisions of "IC Python API:Basic Animation"
From Reallusion Wiki!
Chuck (RL) (Talk | contribs) m |
Chuck (RL) (Talk | contribs) m (→Parametric Algorithm) |
||
| Line 21: | Line 21: | ||
== Parametric Algorithm == | == Parametric Algorithm == | ||
| + | |||
| + | [[File:Ic_python_api_point_on_circumference.png|right|frame]] | ||
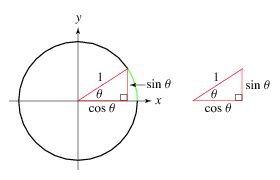
Parametric equations are commonly used to express the coordinates of the points that make up a geometric object such as a curve or surface. In this example, we'll use the following formula to travel along the parameter of a circle: | Parametric equations are commonly used to express the coordinates of the points that make up a geometric object such as a curve or surface. In this example, we'll use the following formula to travel along the parameter of a circle: | ||
| Line 28: | Line 30: | ||
{{Notice|Angle is in radians.}} | {{Notice|Angle is in radians.}} | ||
| + | |||
=== The Code === | === The Code === | ||
Revision as of 19:05, 12 May 2019
- Main article: RL Python Samples.
This article will focus on basic animation with the standard interface of setting the data bloc for the transform controller. However, we will attempt to spice it up with an algorithm for parametric animation.
Preparing the Scene
Prepare an iClone scene for this lesson with the following steps:
- Create a new iClone scene
- Create a ball: Create > Primitive Shape > Sphere.
- Create a cylinder: Create > Primitive Shape > Cylinder.
Required Modules
Only the standard RLPY module is required for this lesson.
import RLPy
Parametric Algorithm
Parametric equations are commonly used to express the coordinates of the points that make up a geometric object such as a curve or surface. In this example, we'll use the following formula to travel along the parameter of a circle:
point.x = origin.x + radius * Cosine( angle )
point.y = origin.y + radius * Sine( angle )
- ⚠ Angle is in radians.
The Code
def parametric_point(center_point, radius, angle):
# Convert angle to radians
a = RLPy.RMath.CONST_DEG_TO_RAD * angle
# Calculate the point on the circumference of a circle
x = center_point.x + radius * RLPy.RMath.Cos(a)
y = center_point.y + radius * RLPy.RMath.Sin(a)
return RLPy.RVector2(x, y)