Difference between revisions of "IC Python API:Basic Animation"

From Reallusion Wiki!
Jump to: navigation, search
m
m
 
(22 intermediate revisions by the same user not shown)
Line 1: Line 1:
 
{{TOC}}
 
{{TOC}}
−
{{Parent|IC_Python_API:RL_Python_Samples|RL Python Samples}}
+
{{Parent|IC_Python_API#Sample_Code_Snippets|RL Python Sample Code Snippets}}
  
 
This article will focus on basic animation with the standard interface of setting the data bloc for the transform controller.  However, we will attempt to spice it up with an algorithm for parametric animation.
 
This article will focus on basic animation with the standard interface of setting the data bloc for the transform controller.  However, we will attempt to spice it up with an algorithm for parametric animation.
Line 9: Line 9:
  
 
# Create a new iClone scene
 
# Create a new iClone scene
−
# Create a ball: Create > Primitive Shape > Sphere.
+
# Create a ball: '''Create > Primitive Shape > Sphere'''.
−
# Create a cylinder: Create > Primitive Shape > Cylinder.
+
# Create a cylinder: '''Create > Primitive Shape > Cylinder'''.
 +
# Move the props apart for better visualization.
  
 
== Required Modules ==
 
== Required Modules ==
Line 21: Line 22:
  
 
== Parametric Algorithm ==
 
== Parametric Algorithm ==
 +
 +
[[File:Ic_python_api_point_on_circumference.png|frame]]
  
 
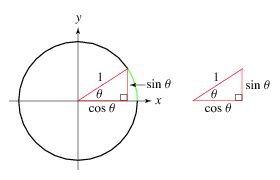
Parametric equations are commonly used to express the coordinates of the points that make up a geometric object such as a curve or surface.  In this example, we'll use the following formula to travel along the parameter of a circle:
 
Parametric equations are commonly used to express the coordinates of the points that make up a geometric object such as a curve or surface.  In this example, we'll use the following formula to travel along the parameter of a circle:
  
−
point.x = origin.x + radius * Cosine( angle )
+
'''''point.x = origin.x + radius * Cosine( angle )'''''
−
<br />point.y = origin.y + radius * Sine( angle )
+
<br />'''''point.y = origin.y + radius * Sine( angle )'''''
  
−
{{Notice|Angle is in radians.}}
+
Keep in mind that '''angle''' is in radians.
  
−
=== The Code ===
+
 
 +
=== Python Code ===
 +
 
 +
The following code will help use retrieve a point on a circumference of a circle based on the position and radius of the circle.  The angle input is the parameter we'll feed into the equation to get a point location output.
  
 
<syntaxhighlight lang="Python">
 
<syntaxhighlight lang="Python">
Line 41: Line 47:
 
     return RLPy.RVector2(x, y)
 
     return RLPy.RVector2(x, y)
 
</syntaxhighlight>
 
</syntaxhighlight>
 +
 +
== Setting up the Props ==
 +
 +
Let's change the way the props are displayed before deploying animation keys.
 +
 +
<syntaxhighlight lang="Python">
 +
# Grab the ball in the scenes: Create > Primitive Shape > Sphere
 +
ball = RLPy.RScene.FindObject(RLPy.EObjectType_Prop, "Ball_000")
 +
# Grab the stick in the scenes: Create > Primitive Shape > Cylinder
 +
stick = RLPy.RScene.FindObject(RLPy.EObjectType_Prop, "Cylinder")
 +
 +
# Get transform control and data block for the ball
 +
ball_control = ball.GetControl("Transform")
 +
ball_db = ball_control.GetDataBlock()
 +
 +
# Get transform control and data block for the stick
 +
stick_control = stick.GetControl("Transform")
 +
stick_db = stick_control.GetDataBlock()
 +
 +
# Setup the stick that spins by laying it on its side and extending its length
 +
time = RLPy.RTime(0)
 +
stick_db.SetData("Position/PositionZ", time, RLPy.RVariant(35))
 +
stick_db.SetData("Rotation/RotationY", time, RLPy.RVariant(90 * RLPy.RMath.CONST_DEG_TO_RAD))
 +
stick_db.SetData("Scale/ScaleX", time, RLPy.RVariant(0.25))
 +
stick_db.SetData("Scale/ScaleY", time, RLPy.RVariant(0.25))
 +
stick_db.SetData("Scale/ScaleZ", time, RLPy.RVariant(1.75))
 +
</syntaxhighlight>
 +
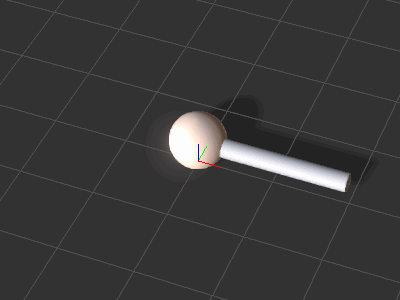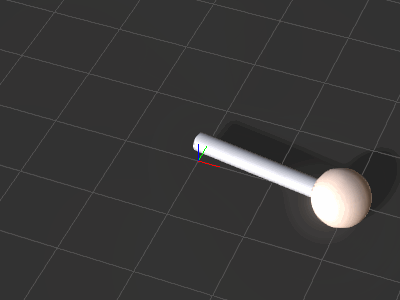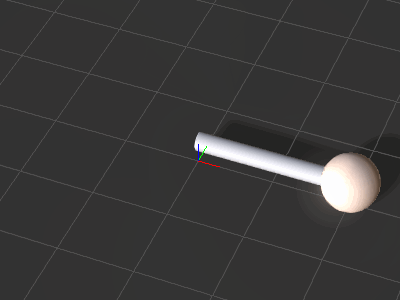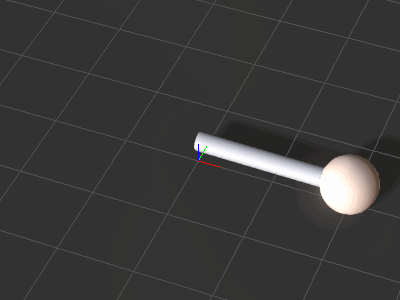
{{Images2
 +
|image1 = Ic_python_api_basic_animation_01.png
 +
|caption1 = The initial scene setup
 +
|image2 = Ic_python_api_basic_animation_02.png
 +
|caption2 = The result after running the script above.
 +
}}
 +
 +
== Animating the Props ==
 +
 +
[[File:Ic_python_api_basic_animation_03.gif|frame|The ball and stick spin as a result. Rotation of the ball is performed with positional keys to match the length of the stick.]]
 +
 +
Let's spin the stick and the ball around in 360 degrees three times.
 +
 +
<syntaxhighlight lang="Python">
 +
degrees = 3 * 360  # Total degrees = revolutions * 360, here we spin 3 times
 +
 +
for i in range(1, degrees):
 +
    time = RLPy.RTime(i * 10)
 +
 +
    # Rotate the stick
 +
    stick_db.SetData("Rotation/RotationX", time, RLPy.RVariant(-i * RLPy.RMath.CONST_DEG_TO_RAD))
 +
 +
    # Move the ball to align with the stick
 +
    position = parametric_point(RLPy.RVector2(0, 0), 200, i)
 +
    ball_db.SetData("Position/PositionX", time, RLPy.RVariant(position.x))
 +
    ball_db.SetData("Position/PositionY", time, RLPy.RVariant(position.y))
 +
 +
# Playback for the entire duration of the animation
 +
RLPy.RGlobal.Play(RLPy.RTime(0), RLPy.RTime(degrees * 10))
 +
</syntaxhighlight>
 +
 +
== Everything Put Together ==
 +
 +
You can copy and paste the following code into a PY file and load it into iClone via '''Script > Load Python'''.
 +
 +
<syntaxhighlight lang="Python">
 +
import RLPy
 +
 +
def parametric_point(center_point, radius, angle):
 +
    # Convert angle to radians
 +
    a = RLPy.RMath.CONST_DEG_TO_RAD * angle
 +
    # Calculate the point on the circumference of a circle
 +
    x = center_point.x + radius * RLPy.RMath.Cos(a)
 +
    y = center_point.y + radius * RLPy.RMath.Sin(a)
 +
 +
    return RLPy.RVector2(x, y)
 +
 +
# Grab the ball in the scenes: Create > Primitive Shape > Sphere
 +
ball = RLPy.RScene.FindObject(RLPy.EObjectType_Prop, "Ball_000")
 +
# Grab the stick in the scenes: Create > Primitive Shape > Cylinder
 +
stick = RLPy.RScene.FindObject(RLPy.EObjectType_Prop, "Cylinder")
 +
 +
# Get transform control and data block for the ball
 +
ball_control = ball.GetControl("Transform")
 +
ball_control.ClearKeys()
 +
ball_db = ball_control.GetDataBlock()
 +
 +
# Get transform control and data block for the stick
 +
stick_control = stick.GetControl("Transform")
 +
stick_control.ClearKeys()
 +
stick_db = stick_control.GetDataBlock()
 +
 +
# Setup the stick that spins by laying it on its side and extending its length
 +
time = RLPy.RTime(0)
 +
stick_db.SetData("Position/PositionZ", time, RLPy.RVariant(35))
 +
stick_db.SetData("Rotation/RotationY", time, RLPy.RVariant(90 * RLPy.RMath.CONST_DEG_TO_RAD))
 +
stick_db.SetData("Scale/ScaleX", time, RLPy.RVariant(0.25))
 +
stick_db.SetData("Scale/ScaleY", time, RLPy.RVariant(0.25))
 +
stick_db.SetData("Scale/ScaleZ", time, RLPy.RVariant(1.75))
 +
 +
degrees = 3 * 360  # Total degrees = revolutions * 360, here we spin 5 times
 +
 +
for i in range(1, degrees):
 +
    time = RLPy.RTime(i * 10)
 +
 +
    # Rotate the stick
 +
    stick_db.SetData("Rotation/RotationX", time, RLPy.RVariant(-i * RLPy.RMath.CONST_DEG_TO_RAD))
 +
 +
    # Move the ball to align with the stick
 +
    position = parametric_point(RLPy.RVector2(0, 0), 200, i)
 +
    ball_db.SetData("Position/PositionX", time, RLPy.RVariant(position.x))
 +
    ball_db.SetData("Position/PositionY", time, RLPy.RVariant(position.y))
 +
 +
# Playback for the entire duration of the animation
 +
RLPy.RGlobal.Play(RLPy.RTime(0), RLPy.RTime(degrees * 10))
 +
</syntaxhighlight>
 +
 +
=== APIs Used ===
 +
You can research the following references for the APIs deployed in this code.
 +
<div style="column-count:4; -moz-column-count:4; -webkit-column-count:4">
 +
* [[ IC_Python_API:RLPy_RMath#Cos | RLPy.RMath.Cos() ]]
 +
* [[ IC_Python_API:RLPy_RMath#Sin | RLPy.RMath.Sin() ]]
 +
* [[ IC_Python_API:RLPy_RVector2 | RLPy.RVector2() ]]
 +
* [[ IC_Python_API:RLPy_RScene#FindObject | RLPy.RScene.FindObject() ]]
 +
* [[ IC_Python_API:RLPy_RTime | RLPy.RTime() ]]
 +
* [[ IC_Python_API:RLPy_RVariant | RLPy.RVariant() ]]
 +
* [[ IC_Python_API:RLPy_RGlobal#Play | RLPy.RGlobal.Play() ]]
 +
</div>

Latest revision as of 19:56, 5 September 2021

Main article: RL Python Sample Code Snippets.

This article will focus on basic animation with the standard interface of setting the data bloc for the transform controller. However, we will attempt to spice it up with an algorithm for parametric animation.

Preparing the Scene

Prepare an iClone scene for this lesson with the following steps:

  1. Create a new iClone scene
  2. Create a ball: Create > Primitive Shape > Sphere.
  3. Create a cylinder: Create > Primitive Shape > Cylinder.
  4. Move the props apart for better visualization.

Required Modules

Only the standard RLPY module is required for this lesson. 

import RLPy

Parametric Algorithm

Ic python api point on circumference.png

Parametric equations are commonly used to express the coordinates of the points that make up a geometric object such as a curve or surface. In this example, we'll use the following formula to travel along the parameter of a circle:

point.x = origin.x + radius * Cosine( angle )
point.y = origin.y + radius * Sine( angle )

Keep in mind that angle is in radians.


Python Code

The following code will help use retrieve a point on a circumference of a circle based on the position and radius of the circle. The angle input is the parameter we'll feed into the equation to get a point location output. 

def parametric_point(center_point, radius, angle):
    # Convert angle to radians
    a = RLPy.RMath.CONST_DEG_TO_RAD * angle
    # Calculate the point on the circumference of a circle
    x = center_point.x + radius * RLPy.RMath.Cos(a)
    y = center_point.y + radius * RLPy.RMath.Sin(a)

    return RLPy.RVector2(x, y)

Setting up the Props

Let's change the way the props are displayed before deploying animation keys. 

# Grab the ball in the scenes: Create > Primitive Shape > Sphere
ball = RLPy.RScene.FindObject(RLPy.EObjectType_Prop, "Ball_000")
# Grab the stick in the scenes: Create > Primitive Shape > Cylinder
stick = RLPy.RScene.FindObject(RLPy.EObjectType_Prop, "Cylinder")

# Get transform control and data block for the ball
ball_control = ball.GetControl("Transform")
ball_db = ball_control.GetDataBlock()

# Get transform control and data block for the stick
stick_control = stick.GetControl("Transform")
stick_db = stick_control.GetDataBlock()

# Setup the stick that spins by laying it on its side and extending its length
time = RLPy.RTime(0)
stick_db.SetData("Position/PositionZ", time, RLPy.RVariant(35))
stick_db.SetData("Rotation/RotationY", time, RLPy.RVariant(90 * RLPy.RMath.CONST_DEG_TO_RAD))
stick_db.SetData("Scale/ScaleX", time, RLPy.RVariant(0.25))
stick_db.SetData("Scale/ScaleY", time, RLPy.RVariant(0.25))
stick_db.SetData("Scale/ScaleZ", time, RLPy.RVariant(1.75))
  • The initial scene setup
  • The result after running the script above.

Animating the Props

The ball and stick spin as a result. Rotation of the ball is performed with positional keys to match the length of the stick.

Let's spin the stick and the ball around in 360 degrees three times. 

degrees = 3 * 360  # Total degrees = revolutions * 360, here we spin 3 times

for i in range(1, degrees):
    time = RLPy.RTime(i * 10)

    # Rotate the stick
    stick_db.SetData("Rotation/RotationX", time, RLPy.RVariant(-i * RLPy.RMath.CONST_DEG_TO_RAD))

    # Move the ball to align with the stick
    position = parametric_point(RLPy.RVector2(0, 0), 200, i)
    ball_db.SetData("Position/PositionX", time, RLPy.RVariant(position.x))
    ball_db.SetData("Position/PositionY", time, RLPy.RVariant(position.y))

# Playback for the entire duration of the animation
RLPy.RGlobal.Play(RLPy.RTime(0), RLPy.RTime(degrees * 10))

Everything Put Together

You can copy and paste the following code into a PY file and load it into iClone via Script > Load Python. 

import RLPy

def parametric_point(center_point, radius, angle):
    # Convert angle to radians
    a = RLPy.RMath.CONST_DEG_TO_RAD * angle
    # Calculate the point on the circumference of a circle
    x = center_point.x + radius * RLPy.RMath.Cos(a)
    y = center_point.y + radius * RLPy.RMath.Sin(a)

    return RLPy.RVector2(x, y)

# Grab the ball in the scenes: Create > Primitive Shape > Sphere
ball = RLPy.RScene.FindObject(RLPy.EObjectType_Prop, "Ball_000")
# Grab the stick in the scenes: Create > Primitive Shape > Cylinder
stick = RLPy.RScene.FindObject(RLPy.EObjectType_Prop, "Cylinder")

# Get transform control and data block for the ball
ball_control = ball.GetControl("Transform")
ball_control.ClearKeys()
ball_db = ball_control.GetDataBlock()

# Get transform control and data block for the stick
stick_control = stick.GetControl("Transform")
stick_control.ClearKeys()
stick_db = stick_control.GetDataBlock()

# Setup the stick that spins by laying it on its side and extending its length
time = RLPy.RTime(0)
stick_db.SetData("Position/PositionZ", time, RLPy.RVariant(35))
stick_db.SetData("Rotation/RotationY", time, RLPy.RVariant(90 * RLPy.RMath.CONST_DEG_TO_RAD))
stick_db.SetData("Scale/ScaleX", time, RLPy.RVariant(0.25))
stick_db.SetData("Scale/ScaleY", time, RLPy.RVariant(0.25))
stick_db.SetData("Scale/ScaleZ", time, RLPy.RVariant(1.75))

degrees = 3 * 360  # Total degrees = revolutions * 360, here we spin 5 times

for i in range(1, degrees):
    time = RLPy.RTime(i * 10)

    # Rotate the stick
    stick_db.SetData("Rotation/RotationX", time, RLPy.RVariant(-i * RLPy.RMath.CONST_DEG_TO_RAD))

    # Move the ball to align with the stick
    position = parametric_point(RLPy.RVector2(0, 0), 200, i)
    ball_db.SetData("Position/PositionX", time, RLPy.RVariant(position.x))
    ball_db.SetData("Position/PositionY", time, RLPy.RVariant(position.y))

# Playback for the entire duration of the animation
RLPy.RGlobal.Play(RLPy.RTime(0), RLPy.RTime(degrees * 10))

APIs Used

You can research the following references for the APIs deployed in this code.

Retrieved from "https://wiki.reallusion.com/index.php?title=IC_Python_API:Basic_Animation&oldid=5335"