Difference between revisions of "IC Python API:RLPy RMatrix4"

From Reallusion Wiki!
Jump to: navigation, search
m
m
 
(4 intermediate revisions by the same user not shown)
Line 5: Line 5:
 
== Description ==
 
== Description ==
  
−
This class represent a standard 3x3 matrix. This class provides access to RLPy's internal 3x3 matrix operators and related functions. iClone uses row-major order where consecutive elements of a row reside next to each other, and the data is read from left to right, top to bottom, in a vertical zig-zag:
+
This class represent the transform data of RTransform. This class provides access to RLPy's internal 4x4 matrix operators and related functions.
  
−
  [0, 1, 2]
+
== Constructor & Destructor ==
−
[3, 4, 5]
+
 
−
[6, 7, 8]
+
=== __init__ ( self, M00 ,M01, M02, M03, M10, M11, M12, M13, M20, M21, M22, M23, M30, M31, M32, M33 ) ===
 +
 
 +
The constructor. Initialize a new [[IC_Python_API:RLPy_RMatrix4|RMatrix4]] with [[IC_Python_API:RLPy_RMatrix4|RMatrix4]] Item Value.
 +
 
 +
==== Parameters ====
 +
:'''M00''' [IN] initialization value - float
 +
:'''M01''' [IN] initialization value - float
 +
:'''M02''' [IN] initialization value - float
 +
:'''M03''' [IN] initialization value - float
 +
:'''M10''' [IN] initialization value - float
 +
:'''M11''' [IN] initialization value - float
 +
:'''M12''' [IN] initialization value - float
 +
:'''M13''' [IN] initialization value - float
 +
:'''M20''' [IN] initialization value - float
 +
:'''M21''' [IN] initialization value - float
 +
:'''M22''' [IN] initialization value - float
 +
:'''M23''' [IN] initialization value - float
 +
:'''M30''' [IN] initialization value - float
 +
:'''M31''' [IN] initialization value - float
 +
:'''M32''' [IN] initialization value - float
 +
:'''M33''' [IN] initialization value - float
 +
 
 +
==== Returns ====
 +
:Returns the row vector of the matrix - [[IC_Python_API:RLPy_RMatrix4|RMatrix4]]
 +
 
 +
<syntaxhighlight lang="python" line='line'>
 +
matrix4 = RLPy.RMatrix4( 1,  2, 3,  4,
 +
                        5,  6,  7,  8,
 +
                        9,  10, 11, 12,
 +
                        13, 14, 15, 16 )
 +
</syntaxhighlight>
 +
 
 +
=== __init__ ( self, Oreder, rx, ty, rz ) ===
 +
 
 +
The constructor. Initialize a new [[IC_Python_API:RLPy_RMatrix4|RMatrix4]] with Order and angle.
 +
 +
==== Parameters ====
 +
:'''Oreder''' [IN] Euler order - RLPy.Rotation_Order
 +
:'''rx''' [IN] Angle of x-axis in radians - float
 +
:'''ry''' [IN] Angle of y-axis in radians - float
 +
:'''rz''' [IN] Angle of z-axis in radians - float
 +
 
 +
==== Returns ====
 +
:Returns the row vector of the matrix - [[IC_Python_API:RLPy_RMatrix4|RMatrix4]]
 +
 
 +
<syntaxhighlight lang="python" line='line'>
 +
euler_angle_x = 90 * RLPy.RMath.CONST_DEG_TO_RAD
 +
euler_angle_y = 0
 +
euler_angle_z = 0
 +
matrix4 = RLPy.RMatrix4( RLPy.EEulerOrder_XYZ, euler_angle_x, euler_angle_y, euler_angle_z )
 +
</syntaxhighlight>
 +
 
 +
=== __init__ ( self, rkRotate ) ===
 +
 
 +
The constructor. Initialize a new [[IC_Python_API:RLPy_RMatrix4|RMatrix4]] with [[IC_Python_API:RLPy_RMatrix3|RMatrix3]].
 +
 
 +
==== Parameters ====
 +
:'''rkRotate''' [IN] Rotation 3x3 matrix - [[IC_Python_API:RLPy_RMatrix3|RMatrix3]]
 +
 
 +
==== Returns ====
 +
:Returns the row vector of the matrix - [[IC_Python_API:RLPy_RMatrix4|RMatrix4]]
 +
 
 +
<syntaxhighlight lang="python" line='line'>
 +
rotate = RLPy.RMatrix3( 1, 0, 0,
 +
                        0, 2, 0,
 +
                        0, 0, 3 )
 +
matrix4 = RLPy.RMatrix4( rotate )
 +
</syntaxhighlight>
 +
 
 +
=== __init__ ( self, kRotate, kTranslate, kScale ) ===
 +
 
 +
The constructor. Initialize a new [[IC_Python_API:RLPy_RMatrix4|RMatrix4]] with RTS.
 +
 
 +
==== Parameters ====
 +
:'''rkRotate''' [IN] Rotation matrix - [[IC_Python_API:RLPy_RMatrix3|RMatrix3]]
 +
:'''rkTranslate''' [IN] Translate vector - [[IC_Python_API:RLPy_RVector3|RVector3]]
 +
:'''rkScale''' [IN] Scale vector - [[IC_Python_API:RLPy_RVector3|RVector3]]
 +
 
 +
==== Returns ====
 +
:Returns the row vector of the matrix - [[IC_Python_API:RLPy_RMatrix4|RMatrix4]]
 +
 
 +
<syntaxhighlight lang="python" line='line'>
 +
rotate = RLPy.RMatrix3( 1, 0, 0,
 +
                        0, 2, 0,
 +
                        0, 0, 3 )
 +
translate = RLPy.RVector3( 1,2,3 )
 +
scale = RLPy.RVector3( 2,2,2 )
 +
matrix4 = RLPy.RMatrix4( rotate, translate, scale )
 +
</syntaxhighlight>
 +
 
 +
=== __init__ ( self, args ) ===
 +
 
 +
The constructor. Initialize a new 4x4 matrix object with another [[IC_Python_API:RLPy_RMatrix4|RMatrix4]] object.
 +
 
 +
==== Parameters ====
 +
:'''args''' [IN] a 4x4 matrix object - [[IC_Python_API:RLPy_RMatrix4|RMatrix4]]
 +
 
 +
==== Returns ====
 +
:Returns the row vector of the matrix - [[IC_Python_API:RLPy_RMatrix4|RMatrix4]]
 +
 
 +
<syntaxhighlight lang="python" line='line'>
 +
matrix4 = RLPy.RMatrix4( 1,  2,  3,  4,
 +
                        5,  6, 7, 8,
 +
                        9,  10, 11, 12,
 +
                        13, 14, 15, 16 )
 +
matrix4_copy = RLPy.RMatrix4( matrix4 )
 +
print( matrix4_copy == matrix4 ) # true
 +
</syntaxhighlight>
  
 
== Operators ==
 
== Operators ==
Line 19: Line 126:
 
See Also: [[#+=|+=]]
 
See Also: [[#+=|+=]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_a = RLPy.RMatrix3( 1, 2, 3,
+
matrix4_a = RLPy.RMatrix4( 1, 2, 3, 4,
−
                           0, 0, 0,
+
                           0, 0, 0, 0,
−
                           0, 0, 0 )
+
                           0, 0, 0, 0,
−
matrix3_b = RLPy.RMatrix3( 2, 2, 2,
+
                          0, 0, 0, 0 )
−
                           0, 0, 0,
+
matrix4_b = RLPy.RMatrix4( 2, 2, 2, 2,
−
                           0, 0, 0 )
+
                           0, 0, 0, 0,
−
matrix3_result = matrix3_a + matrix3_b
+
                           0, 0, 0, 0,
 +
                          0, 0, 0, 0 )
 +
matrix4_result = matrix4_a + matrix4_b
  
−
print( matrix3_result.GetRow(0)[0] == 1+2 ) # true
+
print( matrix4_result.GetRow(0)[0] == 1+2 ) # true
−
print( matrix3_result.GetRow(0)[1] == 2+2 ) # true
+
print( matrix4_result.GetRow(0)[1] == 2+2 ) # true
−
print( matrix3_result.GetRow(0)[2] == 3+2 ) # true
+
print( matrix4_result.GetRow(0)[2] == 3+2 ) # true
 +
print( matrix4_result.GetRow(0)[3] == 4+2 ) # true
 
</syntaxhighlight>
 
</syntaxhighlight>
  
Line 39: Line 149:
 
See Also: [[#-=|-=]]
 
See Also: [[#-=|-=]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_a = RLPy.RMatrix3( 1, 2, 3,
+
matrix4_a = RLPy.RMatrix4( 1, 2, 3, 4,
−
                           0, 0, 0,
+
                           0, 0, 0, 0,
−
                           0, 0, 0 )
+
                           0, 0, 0, 0,
−
matrix3_b = RLPy.RMatrix3( 2, 2, 2,
+
                          0, 0, 0, 0 )
−
                           0, 0, 0,
+
matrix4_b = RLPy.RMatrix4( 2, 2, 2, 2,
−
                           0, 0, 0 )
+
                           0, 0, 0, 0,
−
matrix3_result = matrix3_a - matrix3_b
+
                           0, 0, 0, 0,
 +
                          0, 0, 0, 0 )
 +
matrix4_result = matrix4_a - matrix4_b
  
−
print( matrix3_result.GetRow(0)[0] == 1-2 ) # true
+
print( matrix4_result.GetRow(0)[0] == 1-2 ) # true
−
print( matrix3_result.GetRow(0)[1] == 2-2 ) # true
+
print( matrix4_result.GetRow(0)[1] == 2-2 ) # true
−
print( matrix3_result.GetRow(0)[2] == 3-2 ) # true
+
print( matrix4_result.GetRow(0)[2] == 3-2 ) # true
 +
print( matrix4_result.GetRow(0)[3] == 4-2 ) # true
 
</syntaxhighlight>
 
</syntaxhighlight>
  
 
=== * ===
 
=== * ===
  
−
The "multiplication" operator.
+
The "multiplication" operator.  
  
 
See Also: [[#*=|*=]]
 
See Also: [[#*=|*=]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_a = RLPy.RMatrix3( 1, 2, 3,
+
matrix4_a = RLPy.RMatrix4( 1, 2, 3, 4,
−
                           0, 0, 0,
+
                           0, 0, 0, 0,
−
                           0, 0, 0 )
+
                           0, 0, 0, 0,
−
matrix3_b = RLPy.RMatrix3( 2, 0, 0,
+
                          0, 0, 0, 0 )
−
                           2, 0, 0,
+
matrix4_b = RLPy.RMatrix4( 2, 0, 0, 0,
−
                           2, 0, 0 )
+
                           2, 0, 0, 0,
−
matrix3_result = matrix3_a * matrix3_b
+
                           2, 0, 0, 0,
−
print( matrix3_result.GetRow(0)[0] == 1*2 + 2*2 + 3*2 ) # true
+
                          2, 0, 0, 0 )
 +
matrix4_result = matrix4_a * matrix4_b
 +
 
 +
print( matrix4_result.GetRow(0)[0] == 1*2 + 2*2 + 3*2 + 4*2  ) # true
 
</syntaxhighlight>
 
</syntaxhighlight>
  
 
=== / ===
 
=== / ===
  
−
The "division" operator.  
+
The "division" operator.
  
 
See Also: [[#/=|/=]]
 
See Also: [[#/=|/=]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_a = RLPy.RMatrix3( 1, 2, 3,
+
matrix4_a = RLPy.RMatrix4( 1, 2, 3, 4,
−
                           0, 0, 0,
+
                           0, 0, 0, 0,
−
                           0, 0, 0 )
+
                           0, 0, 0, 0,
−
matrix3_result = matrix3_a / 2
+
                          0, 0, 0, 0 )
 +
matrix4_result = matrix4_a / 2
  
−
print( matrix3_result.GetRow(0)[0] == 1/2 ) # true
+
print( matrix4_result.GetRow(0)[0] == 1/2 ) # true
−
print( matrix3_result.GetRow(0)[1] == 2/2 ) # true
+
print( matrix4_result.GetRow(0)[1] == 2/2 ) # true
−
print( matrix3_result.GetRow(0)[2] == 3/2 ) # true
+
print( matrix4_result.GetRow(0)[2] == 3/2 ) # true
 +
print( matrix4_result.GetRow(0)[3] == 4/2 ) # true
 
</syntaxhighlight>
 
</syntaxhighlight>
  
 
=== - ===
 
=== - ===
  
−
The "unary minus" operator.
+
The "unary minus" .
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_a = RLPy.RMatrix3( 1, 2, 3,
+
matrix4_a = RLPy.RMatrix4( 1, 2, 3, 4,
−
                           0, 0, 0,
+
                           0, 0, 0, 0,
−
                           0, 0, 0 )
+
                           0, 0, 0, 0,
−
matrix3_result = -matrix3_a
+
                          0, 0, 0, 0 )
 +
matrix4_result = -matrix4_a
  
−
print( matrix3_result.GetRow(0)[0] == -1 ) # true
+
print( matrix4_result.GetRow(0)[0] == -1 ) # true
−
print( matrix3_result.GetRow(0)[1] == -2 ) # true
+
print( matrix4_result.GetRow(0)[1] == -2 ) # true
−
print( matrix3_result.GetRow(0)[2] == -3 ) # true
+
print( matrix4_result.GetRow(0)[2] == -3 ) # true
 +
print( matrix4_result.GetRow(0)[3] == -4 ) # true
 
</syntaxhighlight>
 
</syntaxhighlight>
  
Line 108: Line 228:
 
See Also: [[#!=|!=]]
 
See Also: [[#!=|!=]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_a = RLPy.RMatrix3( 1, 2, 3,
+
matrix4_a = RLPy.RMatrix4( 1, 2, 3, 4,
−
                           0, 0, 0,
+
                           0, 0, 0, 0,
−
                           0, 0, 0 )
+
                           0, 0, 0, 0,
−
matrix3_b = RLPy.RMatrix3( 1, 2, 3,
+
                          0, 0, 0, 0 )
−
                           0, 0, 0,
+
matrix4_b = RLPy.RMatrix4( 1, 2, 3, 4,
−
                           0, 0, 0 )
+
                           0, 0, 0, 0,
−
print( matrix3_a == matrix3_b ) # true
+
                           0, 0, 0, 0,
 +
                          0, 0, 0, 0 )
 +
 
 +
print( matrix4_a == matrix4_b ) # true
 
</syntaxhighlight>
 
</syntaxhighlight>
  
Line 124: Line 247:
 
See Also: [[#==|==]]
 
See Also: [[#==|==]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_a = RLPy.RMatrix3( 1, 2, 3,
+
matrix4_a = RLPy.RMatrix4( 1, 2, 3, 4,
−
                           0, 0, 0,
+
                           0, 0, 0, 0,
−
                           0, 0, 0 )
+
                           0, 0, 0, 0,
−
matrix3_b = RLPy.RMatrix3( 4, 5, 6,
+
                          0, 0, 0, 0 )
−
                           0, 0, 0,
+
matrix4_b = RLPy.RMatrix4( 2, 2, 2, 2,
−
                           0, 0, 0 )
+
                           0, 0, 0, 0,
−
print( matrix3_a != matrix3_b ) # true
+
                           0, 0, 0, 0,
 +
                          0, 0, 0, 0 )
 +
 
 +
print( matrix4_a != matrix4_b ) # true
 
</syntaxhighlight>
 
</syntaxhighlight>
  
 
=== > ===
 
=== > ===
  
−
The "greater than" operator. Performs a one-by-one comparison of the matrix array.
+
The "greater than" operator. Performs a one-by-one comparison of the matrix array.
  
 
See Also: [[#>=|>=]]
 
See Also: [[#>=|>=]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_a = RLPy.RMatrix3( 2, 0, 0,
+
matrix4_a = RLPy.RMatrix4( 1, 0, 0, 0,
−
                           0, 0, 0,
+
                           0, 0, 0, 0,
−
                           0, 0, 0 )
+
                           0, 0, 0, 0,
−
matrix3_b = RLPy.RMatrix3( 5, 0, 0,
+
                          0, 0, 0, 0 )
−
                           0, 0, 0,
+
matrix4_b = RLPy.RMatrix4( 2, 0, 0, 0,
−
                           0, 0, 0 )
+
                           0, 0, 0, 0,
−
print( matrix3_b >matrix3_a ) # true
+
                           0, 0, 0, 0,
 +
                          0, 0, 0, 0 )
 +
 
 +
print( matrix4_b > matrix4_a ) # true
 
</syntaxhighlight>
 
</syntaxhighlight>
  
Line 156: Line 285:
 
See Also: [[#>|>]]
 
See Also: [[#>|>]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_a = RLPy.RMatrix3( 1, 1, 3,
+
matrix4_a = RLPy.RMatrix4( 1, 1, 1, 4,
−
                           0, 0, 0,
+
                           0, 0, 0, 0,
−
                           0, 0, 0 )
+
                           0, 0, 0, 0,
−
matrix3_b = RLPy.RMatrix3( 1, 1, 9,
+
                          0, 0, 0, 0 )
−
                           0, 0, 0,
+
matrix4_b = RLPy.RMatrix4( 1, 1, 1, 8,
−
                           0, 0, 0 )
+
                           0, 0, 0, 0,
−
print( matrix3_b >= matrix3_a ) # true
+
                           0, 0, 0, 0,
 +
                          0, 0, 0, 0 )
 +
 
 +
print( matrix4_b >= matrix4_a ) # true
 
</syntaxhighlight>
 
</syntaxhighlight>
  
Line 172: Line 304:
 
See Also: [[#<=|<=]]
 
See Also: [[#<=|<=]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_a = RLPy.RMatrix3( 2, 0, 0,
+
matrix4_a = RLPy.RMatrix4( 2, 0, 0, 0,
−
                           0, 0, 0,
+
                           0, 0, 0, 0,
−
                           0, 0, 0 )
+
                           0, 0, 0, 0,
−
matrix3_b = RLPy.RMatrix3( 5, 0, 0,
+
                          0, 0, 0, 0 )
−
                           0, 0, 0,
+
matrix4_b = RLPy.RMatrix4( 3, 0, 0, 0,
−
                           0, 0, 0 )
+
                           0, 0, 0, 0,
−
print( matrix3_a< matrix3_b ) # true
+
                           0, 0, 0, 0,
 +
                          0, 0, 0, 0 )
 +
 
 +
print( matrix4_a < matrix4_b ) # true
 
</syntaxhighlight>
 
</syntaxhighlight>
  
Line 188: Line 323:
 
See Also: [[#<|<]]
 
See Also: [[#<|<]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_a = RLPy.RMatrix3( 1, 1, 3,
+
matrix4_a = RLPy.RMatrix4( 2, 2, 1, 0,
−
                           0, 0, 0,
+
                           0, 0, 0, 0,
−
                           0, 0, 0 )
+
                           0, 0, 0, 0,
−
matrix3_b = RLPy.RMatrix3( 1, 1, 9,
+
                          0, 0, 0, 0 )
−
                           0, 0, 0,
+
matrix4_b = RLPy.RMatrix4( 2, 2, 5, 0,
−
                           0, 0, 0 )
+
                           0, 0, 0, 0,
−
print( matrix3_a<= matrix3_b ) # true
+
                           0, 0, 0, 0,
 +
                          0, 0, 0, 0 )
 +
 
 +
print( matrix4_a <= matrix4_b ) # true
 
</syntaxhighlight>
 
</syntaxhighlight>
  
Line 204: Line 342:
 
See Also: [[#+|+]]
 
See Also: [[#+|+]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3 =  RLPy.RMatrix3( 1, 2, 3,
+
matrix4 =  RLPy.RMatrix4( 1, 2, 3, 4,
−
                           0, 0, 0,
+
                           0, 0, 0, 0,
−
                           0, 0, 0 )
+
                           0, 0, 0, 0,
−
matrix3 += RLPy.RMatrix3( 2, 2, 2,
+
                          0, 0, 0, 0 )
−
                           0, 0, 0,
+
matrix4 += RLPy.RMatrix4( 2, 2, 2, 2,
−
                           0, 0, 0 )
+
                           0, 0, 0, 0,
 +
                           0, 0, 0, 0,
 +
                          0, 0, 0, 0 )
  
−
print( matrix3.GetRow(0)[0] == 1+2 ) # true
+
print( matrix4.GetRow(0)[0] == 1+2 ) # true
−
print( matrix3.GetRow(0)[1] == 2+2 ) # true
+
print( matrix4.GetRow(0)[1] == 2+2 ) # true
−
print( matrix3.GetRow(0)[2] == 3+2 ) # true
+
print( matrix4.GetRow(0)[2] == 3+2 ) # true
 +
print( matrix4.GetRow(0)[3] == 4+2 ) # true
 
</syntaxhighlight>
 
</syntaxhighlight>
  
Line 223: Line 364:
 
See Also: [[#-|-]]
 
See Also: [[#-|-]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3 =  RLPy.RMatrix3( 1, 2, 3,
+
matrix4 =  RLPy.RMatrix4( 1, 2, 3, 4,
−
                           0, 0, 0,
+
                           0, 0, 0, 0,
−
                           0, 0, 0 )
+
                           0, 0, 0, 0,
−
matrix3 -= RLPy.RMatrix3( 2, 2, 2,
+
                          0, 0, 0, 0 )
−
                           0, 0, 0,
+
matrix4 -= RLPy.RMatrix4( 2, 2, 2, 2,
−
                           0, 0, 0 )
+
                           0, 0, 0, 0,
 +
                           0, 0, 0, 0,
 +
                          0, 0, 0, 0 )
  
−
print( matrix3.GetRow(0)[0] == 1-2 ) # true
+
print( matrix4.GetRow(0)[0] == 1-2 ) # true
−
print( matrix3.GetRow(0)[1] == 2-2 ) # true
+
print( matrix4.GetRow(0)[1] == 2-2 ) # true
−
print( matrix3.GetRow(0)[2] == 3-2 ) # true
+
print( matrix4.GetRow(0)[2] == 3-2 ) # true
 +
print( matrix4.GetRow(0)[3] == 4-2 ) # true
 
</syntaxhighlight>
 
</syntaxhighlight>
  
 
=== *= ===
 
=== *= ===
  
−
The "multiplication assignment" operator.
+
The "multiplication assignment" operator. For the calculation method, refer to the '''*''' operator.
  
 
See Also: [[#*|*]]
 
See Also: [[#*|*]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3 = RLPy.RMatrix3( 1, 2, 3,
+
matrix4 = RLPy.RMatrix4( 1, 2, 3, 4,
−
                          0, 0, 0,
+
                        0, 0, 0, 0,
−
                          0, 0, 0 )
+
                        0, 0, 0, 0,
−
matrix3 *= 2
+
                        0, 0, 0, 0 )
 +
matrix4 *= 2
  
−
print( matrix3.GetRow(0)[0] == 1*2 ) # true
+
print( matrix4.GetRow(0)[0] == 1*2 ) # true
−
print( matrix3.GetRow(0)[1] == 2*2 ) # true
+
print( matrix4.GetRow(0)[1] == 2*2 ) # true
−
print( matrix3.GetRow(0)[2] == 3*2 ) # true
+
print( matrix4.GetRow(0)[2] == 3*2 ) # true
 +
print( matrix4.GetRow(0)[3] == 4*2 ) # true
 
</syntaxhighlight>
 
</syntaxhighlight>
  
 
=== /= ===
 
=== /= ===
  
−
The "division assignment" operator.
+
The "division assignment" operator. For the calculation method, refer to the '''/''' operator.
  
 
See Also: [[#/|/]]
 
See Also: [[#/|/]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3 = RLPy.RMatrix3( 1, 2, 3,
+
matrix4 = RLPy.RMatrix4( 1, 2, 3, 4,
−
                          0, 0, 0,
+
                        0, 0, 0, 0,
−
                          0, 0, 0 )
+
                        0, 0, 0, 0,
−
matrix3 /= 2
+
                        0, 0, 0, 0 )
 +
matrix4 /= 2
  
−
print( matrix3.GetRow(0)[0] == 1/2 ) # true
+
print( matrix4.GetRow(0)[0] == 1/2 ) # true
−
print( matrix3.GetRow(0)[1] == 2/2 ) # true
+
print( matrix4.GetRow(0)[1] == 2/2 ) # true
−
print( matrix3.GetRow(0)[2] == 3/2 ) # true
+
print( matrix4.GetRow(0)[2] == 3/2 ) # true
 +
print( matrix4.GetRow(0)[3] == 4/2 ) # true
 
</syntaxhighlight>
 
</syntaxhighlight>
  
 
== Member Functions ==
 
== Member Functions ==
  
−
=== MakeIdentity ( self ) ===
+
=== MakeIdentity (self) ===
  
 
This function can be used to initialize the 3x3 matrix.  It is equivalent to setting the matrix to:
 
This function can be used to initialize the 3x3 matrix.  It is equivalent to setting the matrix to:
  
−
  [1 0 0]
+
  [1 0 0  0]
−
  [0 1 0]
+
  [0 1 0  0]
−
  [0 0 1]
+
  [0 0 1  0]
 +
[0  0  0  1]
  
 
==== Returns ====
 
==== Returns ====
 +
:This object - [[IC_Python_API:RLPy_RMatrix4|RMatrix4]]
  
−
This object - [[IC_Python_API:RLPy_RMatrix3|RMatrix3]]
+
<syntaxhighlight lang="python" line='line'>
−
 
+
matrix4 = RLPy.RMatrix4()
−
<syntaxhighlight lang="python">
+
matrix4.MakeIdentity()
−
matrix3 = RLPy.RMatrix3()
+
−
matrix3.MakeIdentity()
+
 
</syntaxhighlight>
 
</syntaxhighlight>
  
−
=== M ( self, args ) ===
+
=== M (self, args) ===
  
−
Get the value of an element in a 3x3 matrix by row and column index.
+
Get the value of an element in a 4x4 matrix by row and column index.
  
 
==== Parameters ====
 
==== Parameters ====
Line 298: Line 446:
  
 
==== Returns ====
 
==== Returns ====
−
:The matrix element specified by row and column - float
+
:The matrix element specified by row and col - float
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3 = RLPy.RMatrix3()
+
matrix4 = RLPy.RMatrix4()
−
matrix3.MakeIdentity()
+
matrix4.MakeIdentity()
  
−
print(matrix3.M(0,0)) # <Swig Object of type 'float *' at 0x0000020316B015A0>
+
print(matrix4.M(0,0)) #  
 
</syntaxhighlight>
 
</syntaxhighlight>
  
−
=== E ( self, args ) ===
+
=== E (self, args) ===
  
−
Get the value of an element in a 3x3 matrix by index number (from 0 to 8);
+
Get the value of an element in a 3x3 matrix by index number (from 0 to 15);
  
 
==== Parameters ====
 
==== Parameters ====
Line 317: Line 465:
 
:The matrix element specified by index - float
 
:The matrix element specified by index - float
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3 = RLPy.RMatrix3()
+
matrix4 = RLPy.RMatrix4()
−
matrix3.MakeIdentity()
+
matrix4.MakeIdentity()
  
−
print(matrix3.E(0)) #
+
print(matrix4.E(0)) #  
 
</syntaxhighlight>
 
</syntaxhighlight>
  
−
=== GetRow ( self, nRow ) ===
+
=== GetRow (self, nR) ===
  
−
Retreive a row inside a 3x3 matrix.
+
Retreive a row inside a 4x4 matrix.
  
 
==== Parameters ====
 
==== Parameters ====
−
:'''nRow''' [IN] Index of the row in the matrix - int
+
:'''nRow''' [IN] Index of the row in the matrix.
  
 
==== Returns ====
 
==== Returns ====
−
:The row vector of the matrix - [[IC_Python_API:RLPy_RVector3|RVector3]]
+
:The row vector of the matrix - [[IC_Python_API:RLPy_RVector4|RVector4]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3 = RLPy.RMatrix3()
+
matrix4 = RLPy.RMatrix4()
−
matrix3.MakeIdentity()
+
matrix4.MakeIdentity()
−
row0 = matrix3.GetRow(0)
+
row0 = matrix4.GetRow(0)
  
 
print(row0[0])
 
print(row0[0])
 
print(row0[1])
 
print(row0[1])
 
print(row0[2])
 
print(row0[2])
 +
print(row0[3])
 
</syntaxhighlight>
 
</syntaxhighlight>
  
−
=== GetColumn( self, nCol ) ===
+
=== GetColumn (self, nC) ===
  
−
Retreive a column inside a 3x3 matrix.
+
Retrieve a column inside a 4x4 matrix.
  
 
==== Parameters ====
 
==== Parameters ====
−
:'''nCol''' [IN] Index of the row in the matrix - int
+
:'''nRow''' [IN] Index of the column in the matrix.
  
 
==== Returns ====
 
==== Returns ====
−
:The column vector of the matrix - [[IC_Python_API:RLPy_RVector3|RVector3]]
+
:The column vector of the matrix - [[IC_Python_API:RLPy_RVector4|RVector4]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3 = RLPy.RMatrix3()
+
matrix4 = RLPy.RMatrix4()
−
matrix3.MakeIdentity()
+
matrix4.MakeIdentity()
−
col0 = matrix3.GetColumn(0)
+
col0 = matrix4.GetColumn(0)
  
 
print(col0[0])
 
print(col0[0])
 
print(col0[1])
 
print(col0[1])
 
print(col0[2])
 
print(col0[2])
 +
print(col0[3])
 
</syntaxhighlight>
 
</syntaxhighlight>
  
−
=== Transpose( self ) ===
+
=== Transpose (self) ===
  
 
Obtain the transposed matrix by transposing the current m * n matrix into an n * m matrix by row-column swapping.
 
Obtain the transposed matrix by transposing the current m * n matrix into an n * m matrix by row-column swapping.
  
 
==== Returns ====
 
==== Returns ====
−
:A new matrix containing this matrix's transpose - [[IC_Python_API:RLPy_RMatrix3|RMatrix3]]
+
:A new matrix containing this matrix's transpose - [[IC_Python_API:RLPy_RMatrix4|RMatrix4]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_orgin = RLPy.RMatrix3( 1, 2, 3,
+
matrix4_orgin = RLPy.RMatrix4( 1, 2, 3, 4,
−
                              4, 5, 6,
+
                                5, 6, 7, 8,
−
                              7, 8, 9 )
+
                                9, 10, 11, 12,
−
matrix3_transpose = matrix3_orgin.Transpose()
+
                              13, 14, 15, 16 )
−
row0 = matrix3_orgin.GetRow(0)
+
matrix4_transpose = matrix4_orgin.Transpose()
−
col0 = matrix3_transpose.GetColumn(0)
+
row0 = matrix4_orgin.GetRow(0)
 +
col0 = matrix4_transpose.GetColumn(0)
  
 
print(row0[0] == col0[0])
 
print(row0[0] == col0[0])
 
print(row0[1] == col0[1])
 
print(row0[1] == col0[1])
 
print(row0[2] == col0[2])
 
print(row0[2] == col0[2])
 +
print(row0[3] == col0[3])
 
</syntaxhighlight>
 
</syntaxhighlight>
  
−
=== TransposeTimes( self, mM ) ===
+
=== TransposeTimes (self, mM) ===
  
−
Multiply a transposed version of a 3x3 matrix with itself.
+
Multiply a transposed version of a 4x4 matrix with itself.
  
 
==== Parameters ====
 
==== Parameters ====
−
:'''mM''' [IN] the matrix - [[IC_Python_API:RLPy_RMatrix3|RMatrix3]]
+
:'''mM''' [IN] the matrix - [[IC_Python_API:RLPy_RMatrix4|RMatrix4]]
  
 
==== Returns ====
 
==== Returns ====
−
:A new matrix. (this^T * mM) - [[IC_Python_API:RLPy_RMatrix3|RMatrix3]]
+
:A new matrix. (this^T * mM) - [[IC_Python_API:RLPy_RMatrix4|RMatrix4]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_orgin = RLPy.RMatrix3( 1, 2, 3,
+
matrix4_orgin = RLPy.RMatrix4( 1, 2, 3, 4,
−
                              4, 5, 6,
+
                                5, 6, 7, 8,
−
                              7, 8, 9 )
+
                                9, 10, 11, 12,
−
matrix3_transpose_value = RLPy.RMatrix3( 2, 0, 0,
+
                              13, 14, 15, 16 )
−
                                         0, 2, 0,
+
matrix4_transpose_value = RLPy.RMatrix4( 2, 0, 0, 0,
−
                                         0, 0, 2 )
+
                                         0, 2, 0, 0,
−
matrix3_transpose_times = matrix3_orgin.TransposeTimes(matrix3_transpose_value)
+
                                         0, 0, 2, 0,
−
row0 = matrix3_orgin.GetRow(0)
+
                                        0, 0, 0, 2 )
−
col0 = matrix3_transpose_times.GetColumn(0)
+
matrix4_transpose_times = matrix4_orgin.TransposeTimes(matrix4_transpose_value)
 +
row0 = matrix4_orgin.GetRow(0)
 +
col0 = matrix4_transpose_times.GetColumn(0)
  
 
print(row0[0]*2 == col0[0])
 
print(row0[0]*2 == col0[0])
 
print(row0[1]*2 == col0[1])
 
print(row0[1]*2 == col0[1])
 
print(row0[2]*2 == col0[2])
 
print(row0[2]*2 == col0[2])
 +
print(row0[3]*2 == col0[3])
 
</syntaxhighlight>
 
</syntaxhighlight>
  
−
=== TimesTranspose( self, mM ) ===
+
=== TimesTranspose (self, mM) ===
  
−
Multiply this 3x3 matrix with a transposed version of itself.
+
Multiply this 4x4 matrix with a transposed version of itself.
  
 
==== Parameters ====
 
==== Parameters ====
−
:'''mM''' [IN] the matrix - [[IC_Python_API:RLPy_RMatrix3|RMatrix3]]
+
:'''mM''' [IN] the matrix - [[IC_Python_API:RLPy_RMatrix4|RMatrix4]]
  
 
==== Returns ====
 
==== Returns ====
−
:A new matrix. (this * M^T) - [[IC_Python_API:RLPy_RMatrix3|RMatrix3]]
+
:A new matrix. (this * M^T) - [[IC_Python_API:RLPy_RMatrix4|RMatrix4]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_orgin = RLPy.RMatrix3( 1, 2, 3,
+
matrix4_orgin = RLPy.RMatrix4( 1, 2, 3, 4,
−
                              4, 5, 6,
+
                                5, 6, 7, 8,
−
                              7, 8, 9 )
+
                                9, 10, 11, 12,
−
matrix3_transpose_value = RLPy.RMatrix3( 3, 0, 0,
+
                              13, 14, 15, 16 )
−
                                         0, 3, 0,
+
matrix4_transpose_value = RLPy.RMatrix4( 3, 0, 0, 0,
−
                                         0, 0, 3 )
+
                                         0, 3, 0, 0,
−
matrix3_times_transpose = matrix3_orgin.TimesTranspose(matrix3_transpose_value)
+
                                         0, 0, 3, 0,
−
row0 = matrix3_orgin.GetColumn(0)
+
                                        0, 0, 0, 3 )
−
col0 = matrix3_times_transpose.GetColumn(0)
+
matrix4_times_transpose = matrix4_orgin.TimesTranspose(matrix4_transpose_value)
 +
row0 = matrix4_orgin.GetColumn(0)
 +
col0 = matrix4_times_transpose.GetColumn(0)
  
 
print(row0[0]*3 == col0[0])
 
print(row0[0]*3 == col0[0])
 
print(row0[1]*3 == col0[1])
 
print(row0[1]*3 == col0[1])
 
print(row0[2]*3 == col0[2])
 
print(row0[2]*3 == col0[2])
 +
print(row0[3]*3 == col0[3])
 
</syntaxhighlight>
 
</syntaxhighlight>
  
−
=== Inverse( self ) ===
+
=== Inverse (self) ===
  
−
Obtain the inverse (reciprocal) of this 3x3 matrix (A^-1).
+
Obtain the inverse (reciprocal) of this 4x4 matrix (A^-1).
  
 
==== Returns ====
 
==== Returns ====
−
:A new matrix containing this matrix's inverse - [[IC_Python_API:RLPy_RMatrix3|RMatrix3]]
+
:A new matrix containing this matrix's inverse - [[IC_Python_API:RLPy_RMatrix4|RMatrix4]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_value = RLPy.RMatrix3( 1, 2, 3,
+
matrix4_value = RLPy.RMatrix4( 1, 2, 1, 1,
−
                               2, 3, 4,
+
                               1, 1,-1,-2,
−
                               4, 2, 1 )
+
                              1,-1,-1, 2,
−
matrix3_inverse = matrix3_value.Inverse()
+
                               1,-2, 1,-1 )
−
row0 = matrix3_inverse.GetRow(0)
+
matrix4_inverse = matrix4_value.Inverse()
 +
row0_inverse = matrix4_inverse.GetRow(0)
  
−
print(row0[0])
+
print(row0_inverse[0])
−
print(row0[1])
+
print(row0_inverse[1])
−
print(row0[2])
+
print(row0_inverse[2])
 +
print(row0_inverse[3])
 
</syntaxhighlight>
 
</syntaxhighlight>
  
−
=== Adjoint( self ) ===
+
=== Adjoint (self) ===
  
−
Adjugate this 3x3 matrix.
+
Adjugate this 4x4 matrix.
  
 
==== Returns ====
 
==== Returns ====
−
:A new matrix containing this matrix's adjoint - [[IC_Python_API:RLPy_RMatrix3|RMatrix3]]
+
:A new matrix containing this matrix's adjoint - [[IC_Python_API:RLPy_RMatrix4|RMatrix4]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_value = RLPy.RMatrix3( 1, 2, 3,
+
matrix4_value = RLPy.RMatrix4( 1, 2, 1, 1,
−
                               2, 3, 4,
+
                               1, 1,-1,-2,
−
                               4, 2, 1 )
+
                              1,-1,-1, 2,
−
matrix3_Adjoint = matrix3_value.Adjoint()
+
                               1,-2, 1,-1 )
−
row0 = matrix3_Adjoint.GetRow(0)
+
matrix4_Adjoint = matrix4_value.Adjoint()
 +
row0_Adjoint = matrix4_Adjoint.GetRow(0)
  
−
print(row0[0])
+
print(row0_Adjoint[0])
−
print(row0[1])
+
print(row0_Adjoint[1])
−
print(row0[2])
+
print(row0_Adjoint[2])
 +
print(row0_Adjoint[3])
 
</syntaxhighlight>
 
</syntaxhighlight>
  
−
=== AdjointTranspose( self ) ===
+
=== AdjointTranspose (self) ===
  
−
Adjugate and transpose this 3x3 matrix.
+
Adjugate and transpose this 4x4 matrix.
  
 
==== Returns ====
 
==== Returns ====
−
:A new adjugated and transposed matrix - [[IC_Python_API:RLPy_RMatrix3|RMatrix3]]
+
:A new matrix - [[IC_Python_API:RLPy_RMatrix4|RMatrix4]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_value = RLPy.RMatrix3( 1, 2, 3,
+
matrix4_value = RLPy.RMatrix4( 1, 2, 1, 1,
−
                               2, 3, 4,
+
                               1, 1,-1,-2,
−
                               4, 2, 1 )
+
                              1,-1,-1, 2,
−
matrix3_Adjoint_transpose = matrix3_value.AdjointTranspose()
+
                               1,-2, 1,-1 )
−
col0_Adjoint_transpose = matrix3_Adjoint_transpose.GetColumn(0)
+
matrix4_Adjoint_transpose = matrix4_value.AdjointTranspose()
 +
col0_Adjoint_transpose = matrix4_Adjoint_transpose.GetColumn(0)
  
−
print(col0_Adjoint_transpose[0])
+
print(col0_Adjoint_transpose[0] == row0_Adjoint[0])
−
print(col0_Adjoint_transpose[1])
+
print(col0_Adjoint_transpose[1] == row0_Adjoint[1])
−
print(col0_Adjoint_transpose[2])
+
print(col0_Adjoint_transpose[2] == row0_Adjoint[2])
 +
print(col0_Adjoint_transpose[3] == row0_Adjoint[3])
 
</syntaxhighlight>
 
</syntaxhighlight>
  
−
=== InverseTranspose( self ) ===
+
=== InverseTranspose (self) ===
  
−
Invert and transpose this 3x3 matrix.
+
Invert and transpose this 4x4 matrix.
  
 
==== Returns ====
 
==== Returns ====
−
:A new inverted and transposed matrix - [[IC_Python_API:RLPy_RMatrix3|RMatrix3]]
+
:A new matrix - [[IC_Python_API:RLPy_RMatrix4|RMatrix4]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_value = RLPy.RMatrix3( 1, 2, 3,
+
matrix4_value = RLPy.RMatrix4( 1, 2, 1, 1,
−
                               2, 3, 4,
+
                               1, 1,-1,-2,
−
                               4, 2, 1 )
+
                              1,-1,-1, 2,
−
matrix3_inverse_transpose = matrix3_value.InverseTranspose()
+
                               1,-2, 1,-1 )
−
row0_inverse_transpose = matrix3_inverse_transpose.GetRow(0)
+
matrix4_inverse_transpose = matrix4_value.InverseTranspose()
 +
col0_inverse_transpose = matrix4_inverse_transpose.GetColumn(0)
  
−
print(row0_inverse_transpose[0])
+
print(col0_inverse_transpose[0] == row0_inverse[0])
−
print(row0_inverse_transpose[1])
+
print(col0_inverse_transpose[1] == row0_inverse[1])
−
print(row0_inverse_transpose[2])
+
print(col0_inverse_transpose[2] == row0_inverse[2])
 +
print(col0_inverse_transpose[3] == row0_inverse[3])
 
</syntaxhighlight>
 
</syntaxhighlight>
  
−
=== Determinant( self ) ===
+
=== Determinant (self) ===
  
−
Obtain the scalar value for this 3x3 matrix (|A|).
+
Obtain the scalar value for this 4x4 matrix (|A|).
 +
 
 +
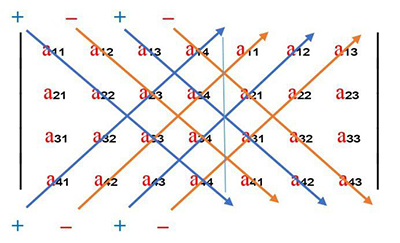
[[File:Rlpy_rmatrix4_determinant.jpg]]
  
 
==== Returns ====
 
==== Returns ====
 
:The determinant of the matrix - float
 
:The determinant of the matrix - float
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_value = RLPy.RMatrix3( 1, 2, 3,
+
matrix4_value = RLPy.RMatrix4( 1, 2, 1, 1,
−
                               2, 3, 4,
+
                               1, 1,-1,-2,
−
                               4, 2, 1 )
+
                              1,-1,-1, 2,
−
 
+
                               1,-2, 1,-1 )
−
print(matrix3_value.Determinant())
+
print(matrix4_value.Determinant())
 
</syntaxhighlight>
 
</syntaxhighlight>
  
−
=== MaxColumn( self ) ===
+
=== MaxColumn (self) ===
  
−
Find the maximum absolute value within this 3x3 matrix, and return the column in which the value is located.  If all of the elements within the 3x3 matrix are 0 then return -1.
+
Find the maximum absolute value within this 4x4 matrix, and return the column in which the value is located.  If all of the elements within the 4x4 matrix are 0 then return -1.
  
 
==== Returns ====
 
==== Returns ====
−
:Index of column of M containing maximum abs entry, or -1 if M = 0 - int
+
:Return index of column of M containing maximum abs entry, or -1 if M = 0 - int
−
 
+
−
<syntaxhighlight lang="python">
+
−
matrix3_value = RLPy.RMatrix3( 10, 20, -30,
+
−
                                0,  0,  0,
+
−
                                0,  0,  0 )
+
  
−
print(matrix3_value.MaxColumn()) # column:2 ->abs(-30)
+
<syntaxhighlight lang="python" line='line'>
 +
matrix4_column_value = RLPy.RMatrix4( 1, 2, 3,-5,
 +
                                      0, 0, 0, 0,
 +
                                      0, 0, 0, 0,
 +
                                      0, 0, 0, 0 )
 +
print(matrix4_column_value.MaxColumn()) # column:3 -> abs(-5)
 
</syntaxhighlight>
 
</syntaxhighlight>
  
−
=== MaxRow( self ) ===
+
=== MaxRow (self) ===
  
−
Find the maximum absolute value within this 3x3 matrix, and return the row in which the value is located.  If all of the elements within the 3x3 matrix are 0 then return -1.
+
Find the maximum absolute value within this 4x4 matrix, and return the row in which the value is located.  If all of the elements within the 4x4 matrix are 0 then return -1.
  
 
==== Returns ====
 
==== Returns ====
−
:Index of row of M containing maximum abs entry, or -1 if M = 0 - int
+
:Return index of row of M containing maximum abs entry, or -1 if M = 0 - int
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_value = RLPy.RMatrix3( 10, 0, 0,
+
matrix4_row_value = RLPy.RMatrix4( 1, 0, 0, 0,
−
                              20, 0, 0,
+
                                  2, 0, 0, 0,
−
                              -30, 0, 0 )
+
                                  3, 0, 0, 0,
−
print(matrix3_value.MaxRow()) # Row:2 ->abs(-30)
+
                                  -5, 0, 0, 0 )
 +
print(matrix4_value.MaxRow()) # Row:3 -> abs(-5)
 
</syntaxhighlight>
 
</syntaxhighlight>
  
−
=== OneNorm( self ) ===
+
=== OneNorm (self) ===
  
 
Return the sum of the column elements that contain the largest absolute values.
 
Return the sum of the column elements that contain the largest absolute values.
  
 
==== Returns ====
 
==== Returns ====
−
:Norm of this 3x3 matrix - float
+
:Return Norm - float
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_row_value = RLPy.RMatrix3( 10, 0, 0,
+
matrix4_row_value = RLPy.RMatrix4( 1, 0, 0, 0,
−
                                   20, 0, 0,
+
                                   2, 0, 0, 0,
−
                                   -30, 0, 0 )
+
                                  3, 0, 0, 0,
−
print(matrix3_row_value.OneNorm()) # 10+20+abs(-30) = 60
+
                                   -5, 0, 0, 0 )
 +
print(matrix4_row_value.OneNorm()) # 11 -> 1+2+abs(-5)
 
</syntaxhighlight>
 
</syntaxhighlight>
  
−
=== InfNorm( self ) ===
+
=== InfNorm (self) ===
  
 
Return the sum of the row elements that contain the largest absolute values.
 
Return the sum of the row elements that contain the largest absolute values.
  
 
==== Returns ====
 
==== Returns ====
−
:InfNorm of this 3x3 matrix - float
+
:Return InfNorm - float
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_column_value = RLPy.RMatrix3( 10, 20, -30,
+
matrix4_column_value = RLPy.RMatrix4( 1, 2, 3,-5,
−
                                      0, 0,   0,
+
                                      0, 0, 0, 0,
−
                                      0, 0,   0 )
+
                                      0, 0, 0, 0,
−
print(matrix3_column_value.InfNorm()) # 10+20+abs(-30) = 60
+
                                      0, 0, 0, 0 )
 +
print(matrix4_column_value.InfNorm()) # 11 -> 1+2+abs(-5)
 
</syntaxhighlight>
 
</syntaxhighlight>
  
−
=== FromAxisAngle( self, rkAxis, fAngle ) ===
+
=== FromRTS (self, kRotate, kTranslate, kScale) ===
  
−
Rotation matrix from axis angle。
+
Apply rotate, translate, and scale data to a 4x4 matrix.
  
 
==== Parameters ====
 
==== Parameters ====
−
:'''rkAxis''' [IN] axis vector - [[IC_Python_API:RLPy_RVector3|RVector3]]
+
:'''kRotate  ''' [IN] Rotate Matrix - [[IC_Python_API:RLPy_RMatrix3|RMatrix3]]
−
:'''fAngle''' [IN] angle in radians - float
+
:'''kTranslate''' [IN] Translate vector - [[IC_Python_API:RLPy_RVector3|RVector3]]
 +
:'''kScale  ''' [IN] Scale vector - [[IC_Python_API:RLPy_RVector3|RVector3]]
  
 
==== Returns ====
 
==== Returns ====
−
:A new matrix from specified axis angle - [[IC_Python_API:RLPy_RMatrix3|RMatrix3]]
+
:Return a new matrix from RTS - [[IC_Python_API:RLPy_RMatrix4|RMatrix4]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_orgin = RLPy.RMatrix3()
+
rotate = RLPy.RMatrix3( 1, 0, 0,
−
matrix3_orgin.MakeIdentity()
+
                        0, 1, 0,
 +
                        0, 0, 1 )
 +
translate = RLPy.RVector3( 1, 0, 0 )
 +
scale = RLPy.RVector3( 2, 2, 2 )
 +
matrix4_result =  RLPy.RMatrix4().FromRTS( rotate, translate, scale )
 +
row0 = matrix4_result.GetRow(0)
  
−
x_axis_vector = RLPy.RVector3( 1, 0, 0 )  # axis = "X"
+
print(row0[0])
−
y_axis_vector = RLPy.RVector3( 0, 1, 0 ) # axis = "Y"
+
print(row0[1])
−
z_axis_vector = RLPy.RVector3( 0, 0, 1 ) # axis = "Z"   
+
print(row0[2])
 +
print(row0[3])
 +
</syntaxhighlight>
 +
 
 +
=== GetSimpleRTS (self, rkRotate, rkTranslate, rkScale) ===
 +
 
 +
Retrieve rotation, translation, and scale data from this 4x4 matrix.
 +
 
 +
==== Parameters ====
 +
:'''rkRotate''' [IN] Angle of x-axis in radians - float
 +
:'''rkTranslate''' [IN] Angle of y-axis in radians - float
 +
:'''rkScale  ''' [IN] Angle of z-axis in radians - float
 +
 
 +
==== Returns ====
 +
 
 +
<syntaxhighlight lang="python" line='line'>
 +
matrix4_value = RLPy.RMatrix4( 1, 2, 1, 1,
 +
                              1, 1,-1,-2,
 +
                              1,-1,-1, 2,
 +
                              1,-2, 1,-1 )
 +
rotate = RLPy.RMatrix3()
 +
translate = RLPy.RVector3()
 +
scale = RLPy.RVector3()
 +
matrix4_value.GetSimpleRTS( rotate, translate, scale )
 +
row0 = rotate.GetRow(0)
 +
 
 +
print(row0[0])
 +
print(row0[1])
 +
print(row0[2])
 +
 
 +
print(translate[0])
 +
print(translate[1])
 +
print(translate[2])
  
−
matrix3_orgin.FromAxisAngle( x_axis_vector, 90 * RLPy.RMath.CONST_DEG_TO_RAD )
+
print(scale[0])
−
matrix3_orgin.FromAxisAngle( y_axis_vector, 90 * RLPy.RMath.CONST_DEG_TO_RAD )
+
print(scale[1])
−
matrix3_orgin.FromAxisAngle( z_axis_vector, 90 * RLPy.RMath.CONST_DEG_TO_RAD )
+
print(scale[2])      
 
</syntaxhighlight>
 
</syntaxhighlight>
  
−
=== RotationX( self, fAngle ) ===
+
=== GetSimpleRotate (self, rkRotate) ===
  
−
Rotate this 3x3 matrix around the x-axis.
+
Retrieve rotation data from this 4x4 matrix.
  
 
==== Parameters ====
 
==== Parameters ====
−
fAngle  [IN] angle in radians - float
+
:'''rkRotate''' [IN] Rotation Matrix - [[IC_Python_API:RLPy_RMatrix3|RMatrix3]]
  
 
==== Returns ====
 
==== Returns ====
−
:The rotated 3x3 matrix around the x-axis - [[IC_Python_API:RLPy_RMatrix3|RMatrix3]]
+
:3x3 matrix rotation data of this 4x4 matrix.
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_orgin = RLPy.RMatrix3()
+
matrix4_value = RLPy.RMatrix4( 1, 2, 1, 1,
−
matrix3_orgin.MakeIdentity()
+
                              1, 1,-1,-2,
−
matrix3_orgin.RotationX( 90 * RLPy.RMath.CONST_DEG_TO_RAD )
+
                              1,-1,-1, 2,
 +
                              1,-2, 1,-1
 +
rotate = RLPy.RMatrix3()
 +
matrix4_value.GetSimpleRotate( rotate )
 +
row0 = rotate.GetRow(0)
 +
 
 +
print(row0[0])
 +
print(row0[1])
 +
print(row0[2])
 
</syntaxhighlight>
 
</syntaxhighlight>
  
−
=== RotationY( self, fAngle ) ===
+
=== SetTranslateZero (self) ===
  
−
Rotate this 3x3 matrix around the y-axis。
+
Set the translation data in this 4x4 matrix to 0.
 +
 
 +
<syntaxhighlight lang="python" line='line'>
 +
matrix4_value = RLPy.RMatrix4( 1, 2, 1, 1,
 +
                              1, 1,-1,-2,
 +
                              1,-1,-1, 2,
 +
                              1,-2, 1,-1
 +
matrix4_value.SetTranslateZero()
 +
row3 = matrix4_value.GetRow(3)
 +
 
 +
print(row3[0] == 0)
 +
print(row3[1] == 0)
 +
print(row3[2] == 0)
 +
</syntaxhighlight>
 +
 
 +
=== RotationX (self, fAngle) ===
 +
 
 +
Rotation matrix for rotations around x-axis.
  
 
==== Parameters ====
 
==== Parameters ====
Line 632: Line 866:
  
 
==== Returns ====
 
==== Returns ====
−
:The rotated 3x3 matrix around the y-axis - [[IC_Python_API:RLPy_RMatrix3|RMatrix3]]
+
:Return a new matrix of for rotations around x-axis - [[IC_Python_API:RLPy_RMatrix4|RMatrix4]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_orgin = RLPy.RMatrix3()
+
matrix4_orgin = RLPy.RMatrix4()
−
matrix3_orgin.MakeIdentity()
+
matrix4_orgin.MakeIdentity()
−
matrix3_orgin.RotationY( 90 * RLPy.RMath.CONST_DEG_TO_RAD )
+
matrix4_orgin.RotationX( 90 * RLPy.RMath.CONST_DEG_TO_RAD )
 
</syntaxhighlight>
 
</syntaxhighlight>
  
−
=== RotationZ( self, fAngle ) ===
+
=== RotationY (self, fAngle) ===
  
−
Rotation this 3x3 matrix around the z-axis.
+
Rotation matrix for rotations around y-axis.
  
 
==== Parameters ====
 
==== Parameters ====
Line 648: Line 882:
  
 
==== Returns ====
 
==== Returns ====
−
:A new 3x3 matrix of for rotations around z-axis - [[IC_Python_API:RLPy_RMatrix3|RMatrix3]]
+
:Return a new matrix of for rotations around y-axis - [[IC_Python_API:RLPy_RMatrix4|RMatrix4]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_orgin = RLPy.RMatrix3()
+
matrix4_orgin = RLPy.RMatrix4()
−
matrix3_orgin.MakeIdentity()
+
matrix4_orgin.MakeIdentity()
−
matrix3_orgin.RotationZ( 90 * RLPy.RMath.CONST_DEG_TO_RAD )
+
matrix4_orgin.RotationY( 90 * RLPy.RMath.CONST_DEG_TO_RAD )
 
</syntaxhighlight>
 
</syntaxhighlight>
  
−
=== AccuScale( self, rkScale ) ===
+
=== RotationZ (self, fAngle) ===
  
−
Accumulate 3x3 matrix with scale vector.
+
Rotation matrix for rotations around z-axis.
  
 
==== Parameters ====
 
==== Parameters ====
−
rkScale [IN] Scale vector - [[IC_Python_API:RLPy_RVector3|RVector3]]
+
:'''fAngle''' [IN] angle in radians - float
  
 
==== Returns ====
 
==== Returns ====
−
:A newly scaled matrix - [[IC_Python_API:RLPy_RMatrix3|RMatrix3]]
+
:Return a new matrix of for rotations around z-axis - [[IC_Python_API:RLPy_RMatrix4|RMatrix4]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_orgin = RLPy.RMatrix3()
+
matrix4_orgin = RLPy.RMatrix4()
−
matrix3_orgin.MakeIdentity()
+
matrix4_orgin.MakeIdentity()
−
scale_vector = RLPy.RVector3( 2, 2, 2 )
+
matrix4_orgin.RotationZ( 90 * RLPy.RMath.CONST_DEG_TO_RAD )
−
matrix3_orgin.AccuScale(scale_vector)
+
 
</syntaxhighlight>
 
</syntaxhighlight>
  
−
=== ToEulerAngle( self, rkScaleself, Order, rx, ry, rz ) ===
+
=== RotateAxisAngle (self, rkAxis, fAngle) ===
  
−
Convert 3x3 matrix to Euler angles.
+
Rotation matrix from axis angle.
  
 
==== Parameters ====
 
==== Parameters ====
−
:'''Order''' [IN] Euler order - RLPy.Rotation_Order
+
:'''rkAxis''' [IN] axis vector - [[IC_Python_API:RLPy_RVector3|RVector3]]
−
:'''rx''' [OUT] Angle of x-axis in radians - float
+
:'''fAngle''' [IN] angle in radians - float
−
:'''ry''' [OUT] Angle of y-axis in radians - float
+
−
:'''rz''' [OUT] Angle of z-axis in radians - float
+
  
−
<syntaxhighlight lang="python">
+
==== Returns ====
−
matrix3_value = RLPy.RMatrix3( -0, -0,  1,
+
:Return a new matrix from specified axis angle - [[IC_Python_API:RLPy_RMatrix4|RMatrix4]]
−
                                0, -1, -0,
+
−
                                1,  0, -0 )
+
−
euler_angle_x = 0
+
−
euler_angle_y = 0
+
−
euler_angle_z = 0
+
−
result = matrix3_value.ToEulerAngle( RLPy.EEulerOrder_XYZ, euler_angle_x, euler_angle_y, euler_angle_z )
+
  
−
print(result[0] * RLPy.RMath.CONST_RAD_TO_DEG) # 180
+
<syntaxhighlight lang="python" line='line'>
−
print(result[1] * RLPy.RMath.CONST_RAD_TO_DEG) # 90
+
matrix4_value = RLPy.RMatrix4( 1, 2, 1, 1,
−
print(result[2] * RLPy.RMath.CONST_RAD_TO_DEG) # 0
+
                              1, 1,-1,-2,
 +
                              1,-1,-1, 2,
 +
                              1,-2, 1,-1
 +
x_axis_vector = RLPy.RVector3( 1, 0, 0 )  # axis = "X"
 +
y_axis_vector = RLPy.RVector3( 0, 1, 0 ) # axis = "Y"
 +
z_axis_vector = RLPy.RVector3( 0, 0, 1 )  # axis = "Z"   
 +
matrix4_value.RotateAxisAngle( x_axis_vector, 90 * RLPy.RMath.CONST_DEG_TO_RAD )
 +
matrix4_value.RotateAxisAngle( y_axis_vector, 90 * RLPy.RMath.CONST_DEG_TO_RAD )
 +
matrix4_value.RotateAxisAngle( z_axis_vector, 90 * RLPy.RMath.CONST_DEG_TO_RAD )
 
</syntaxhighlight>
 
</syntaxhighlight>
  
−
=== FromEulerAngle( self, Order, rx, ry, rz ) ===
+
=== FromEulerAngle (self, Oreder, rx, ry, rz) ===
  
−
Convert Euler angle to a 3x3 matrix according to a rotation axis order.
+
Convert Euler angle to a 4x4 matrix according to a rotation axis order.
  
 
==== Parameters ====
 
==== Parameters ====
−
:'''Order''' [IN] Euler order - RLPy.Rotation_Order
+
:'''Oreder''' [IN] Euler order - RLPY.EEulerOrder
 +
:*EEulerOrder_XYZ = _RLPy.EEulerOrder_XYZ
 +
:*EEulerOrder_ZYX = _RLPy.EEulerOrder_ZYX
 +
:*EEulerOrder_XZY = _RLPy.EEulerOrder_XZY
 +
:*EEulerOrder_YZX = _RLPy.EEulerOrder_YZX
 +
:*EEulerOrder_YXZ = _RLPy.EEulerOrder_YXZ
 +
:*EEulerOrder_ZXY = _RLPy.EEulerOrder_ZXY
 
:'''rx''' [IN] Angle of x-axis in radians - float
 
:'''rx''' [IN] Angle of x-axis in radians - float
 
:'''ry''' [IN] Angle of y-axis in radians - float
 
:'''ry''' [IN] Angle of y-axis in radians - float
Line 708: Line 947:
  
 
==== Returns ====
 
==== Returns ====
−
:A new matrix from specified axis angle - [[IC_Python_API:RLPy_RMatrix3|RMatrix3]]
+
:Return a new matrix from specified axis angle - [[IC_Python_API:RLPy_RMatrix4|RMatrix4]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_orgin = RLPy.RMatrix3()
+
 
euler_angle_x = 90 * RLPy.RMath.CONST_DEG_TO_RAD
 
euler_angle_x = 90 * RLPy.RMath.CONST_DEG_TO_RAD
 
euler_angle_y = 0
 
euler_angle_y = 0
 
euler_angle_z = 0
 
euler_angle_z = 0
−
matrix3_result = matrix3_orgin.FromEulerAngle( RLPy.EEulerOrder_XYZ, euler_angle_x, euler_angle_y, euler_angle_z)
+
matrix4_result = RLPy.RMatrix4().FromEulerAngle( RLPy.EEulerOrder_XYZ, euler_angle_x, euler_angle_y, euler_angle_z)
−
row0 = matrix3_result[0].GetRow(0)
+
row0 = matrix4_result[0].GetRow(0)
  
 
print(row0[0])
 
print(row0[0])
 
print(row0[1])
 
print(row0[1])
 
print(row0[2])
 
print(row0[2])
 +
print(row0[3])
 
</syntaxhighlight>
 
</syntaxhighlight>
  
−
=== FromSphereUnitVec( self, rkVec ) ===
+
=== SetSR (self, mSR) ===
  
−
Convert Euler angle to matrix.
+
Set scale and rotation part of the matrix.
  
 
==== Parameters ====
 
==== Parameters ====
−
:'''rkVec''' [IN] vector - [[IC_Python_API:RLPy_RVector3|RVector3]]
+
:'''mSR''' [IN] 3x3 matrix - [[IC_Python_API:RLPy_RMatrix3|RMatrix3]]
  
 
==== Returns ====
 
==== Returns ====
−
:A new 3x3 matrix from sphere unit vector - [[IC_Python_API:RLPy_RMatrix3|RMatrix3]]
+
:Return a new 4x4 matrix - [[IC_Python_API:RLPy_RMatrix4|RMatrix4]]
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
vector = RLPy.RVector3( 0, 1, 0 )
+
matrix4_orgin = RLPy.RMatrix4()
−
matrix3_result = RLPy.RMatrix3().FromSphereUnitVec( vector )
+
matrix4_orgin.MakeIdentity()
−
row0 = matrix3_result.GetRow(0)
+
matrix3_rotate_value = RLPy.RMatrix3( 1, 0, 0,
 +
                                      0, 1, 0,
 +
                                      0, 0, 1 )
 +
matrix4_orgin.SetSR(matrix3_rotate_value)
 +
</syntaxhighlight>
 +
 
 +
=== GetSR (self) ===
 +
 
 +
Get scale and rotation part of the matrix.
 +
 
 +
==== Returns ====
 +
:Return a 3x3 matrix - [[IC_Python_API:RLPy_RMatrix3|RMatrix3]]
  
 +
<syntaxhighlight lang="python" line='line'>
 +
matrix4_value = RLPy.RMatrix4( 1, 2, 1, 1,
 +
                              1, 1,-1,-2,
 +
                              1,-1,-1, 2,
 +
                              1,-2, 1,-1
 +
result = matrix4_value.GetSR()
 +
row0 = result.GetRow(0)
 
print(row0[0])
 
print(row0[0])
 
print(row0[1])
 
print(row0[1])
Line 743: Line 1,000:
 
</syntaxhighlight>
 
</syntaxhighlight>
  
−
=== IsRightHandCoordinate( self ) ===
+
=== SetTranslate (self, vTranslate) ===
  
−
Obtain this 3x3 matrix's coordinate system. '''True''' stands for right-handed coordinate system while '''False''' for left-handed.
+
Set translate of the matrix.
 +
 
 +
==== Parameters ====
 +
:'''vTranslate''' [IN] Translate vector - [[IC_Python_API:RLPy_RVector3|RVector3]]
  
 
==== Returns ====
 
==== Returns ====
−
:'''True''' Right hand coordinate - bool
+
:New matrix with the specified translation - [[IC_Python_API:RLPy_RMatrix4|RMatrix4]]
−
:'''False''' Left hand coordinate - bool
+
  
−
<syntaxhighlight lang="python">
+
<syntaxhighlight lang="python" line='line'>
−
matrix3_value = RLPy.RMatrix3( 1, 0, 0,
+
matrix4_orgin = RLPy.RMatrix4()
−
                              0, 1, 0,
+
matrix4_orgin.MakeIdentity()
−
                              0, 0, 1 )
+
matrix4_orgin.SetTranslate(RLPy.RVector3( 1, 2, 3 ) )
−
result = matrix3_value.IsRightHandCoordinate()
+
</syntaxhighlight>
 +
 
 +
=== GetTranslate (self) ===
 +
 
 +
Get translate of the matrix.
 +
 
 +
==== Returns ====
 +
:Return a translate vector - [[IC_Python_API:RLPy_RVector3|RVector3]]
 +
 
 +
<syntaxhighlight lang="python" line='line'>
 +
matrix4_orgin = RLPy.RMatrix4()
 +
matrix4_orgin.MakeIdentity()
 +
matrix4_orgin.SetTranslate(RLPy.RVector3( 1, 2, 3 ) )
 +
result = matrix4_orgin.GetTranslate()
 +
 
 +
print(result[0] == 1)
 +
print(result[1] == 2)
 +
print(result[2] == 3)
 +
</syntaxhighlight>
 +
 
 +
=== AccuScale (self, rkScale) ===
 +
 
 +
Accumulate this 4x4 matrix with scale vector.
 +
 
 +
==== Parameters ====
 +
:'''rkScale''' [IN] Scale vector - [[IC_Python_API:RLPy_RVector3|RVector3]]
 +
 
 +
==== Returns ====
 +
:Accumulate of this 4x4 matrix with scale vector - [[IC_Python_API:RLPy_RMatrix4|RMatrix4]]
 +
 
 +
<syntaxhighlight lang="python" line='line'>
 +
matrix4_orgin = RLPy.RMatrix4()
 +
matrix4_orgin.MakeIdentity()
 +
matrix4_orgin.AccuScale(RLPy.RVector3( 2, 2, 2 ) )
 +
matrix4_orgin.AccuScale(RLPy.RVector3( 3, 3, 3 ) )
 +
result = matrix4_orgin.GetSR()
 +
row0 = result.GetRow(0)
 +
print(row0[0] == 2*3)
 +
row1 = result.GetRow(1)
 +
print(row1[1] == 2*3)
 +
row2 = result.GetRow(2)
 +
print(row2[2] == 2*3)
 +
</syntaxhighlight>
 +
 
 +
=== AccuRotate (self, rkRotate) ===
 +
 
 +
Accumulate this 4x4 matrix with rotation matrix.
 +
 
 +
==== Parameters ====
 +
:'''rkRotate''' [IN] Rotation matrix - [[IC_Python_API:RLPy_RMatrix3|RMatrix3]]
 +
 
 +
==== Returns ====
 +
:Accumulate this 4x4 matrix and rotation matrix - [[IC_Python_API:RLPy_RMatrix4|RMatrix4]]
 +
 
 +
<syntaxhighlight lang="python" line='line'>
 +
matrix4_orgin = RLPy.RMatrix4()
 +
matrix4_orgin.MakeIdentity()
 +
matrix3_orgin = RLPy.RMatrix3()
 +
matrix3_orgin.FromAxisAngle( RLPy.RVector3( 0, 1, 0 ), 90 * RLPy.RMath.CONST_DEG_TO_RAD )
 +
matrix4_orgin.AccuRotate(matrix3_orgin)
 +
matrix4_orgin.AccuRotate(matrix3_orgin)
 +
rotate = RLPy.RMatrix3()
 +
matrix4_orgin.GetSimpleRotate( rotate )
 +
row0 = rotate.GetRow(0)
 +
print(row0[0])
 +
print(row0[1])
 +
print(row0[2])
 +
</syntaxhighlight>
 +
 
 +
=== AccuTranslate (self, rkTranslate) ===
 +
 
 +
Accumulate this 4x4 matrix with translate vector.
 +
 
 +
==== Parameters ====
 +
:'''rkTranslate''' [IN] Translate vector - [[IC_Python_API:RLPy_RVector3|RVector3]]
 +
 
 +
==== Returns ====
 +
:Accumulate of this 4x4 matrix and translation vector - [[IC_Python_API:RLPy_RMatrix4|RMatrix4]]
  
−
print(result)
+
<syntaxhighlight lang="python" line='line'>
 +
matrix4_orgin = RLPy.RMatrix4()
 +
matrix4_orgin.MakeIdentity()
 +
matrix4_orgin.AccuTranslate(RLPy.RVector3( 1, 2, 3 ) )
 +
matrix4_orgin.AccuTranslate(RLPy.RVector3( 2, 2, 2 ) )
 +
row3 = matrix4_orgin.GetRow(3)
 +
print(row3[0] == 1+2)
 +
print(row3[1] == 2+2)
 +
print(row3[2] == 2+3)
 
</syntaxhighlight>
 
</syntaxhighlight>

Latest revision as of 23:48, 14 April 2020

Contents

Main article: Modules.
Last modified: 04/14/2020

Description

This class represent the transform data of RTransform. This class provides access to RLPy's internal 4x4 matrix operators and related functions.

Constructor & Destructor

__init__ ( self, M00 ,M01, M02, M03, M10, M11, M12, M13, M20, M21, M22, M23, M30, M31, M32, M33 )

The constructor. Initialize a new RMatrix4 with RMatrix4 Item Value.

Parameters

M00 [IN] initialization value - float
M01 [IN] initialization value - float
M02 [IN] initialization value - float
M03 [IN] initialization value - float
M10 [IN] initialization value - float
M11 [IN] initialization value - float
M12 [IN] initialization value - float
M13 [IN] initialization value - float
M20 [IN] initialization value - float
M21 [IN] initialization value - float
M22 [IN] initialization value - float
M23 [IN] initialization value - float
M30 [IN] initialization value - float
M31 [IN] initialization value - float
M32 [IN] initialization value - float
M33 [IN] initialization value - float

Returns

Returns the row vector of the matrix - RMatrix4 
1 matrix4 = RLPy.RMatrix4( 1,   2,  3,  4,
2                          5,   6,  7,  8,
3                          9,  10, 11, 12,
4                          13, 14, 15, 16 )

__init__ ( self, Oreder, rx, ty, rz )

The constructor. Initialize a new RMatrix4 with Order and angle.

Parameters

Oreder [IN] Euler order - RLPy.Rotation_Order
rx [IN] Angle of x-axis in radians - float
ry [IN] Angle of y-axis in radians - float
rz [IN] Angle of z-axis in radians - float

Returns

Returns the row vector of the matrix - RMatrix4 
1 euler_angle_x = 90 * RLPy.RMath.CONST_DEG_TO_RAD
2 euler_angle_y = 0
3 euler_angle_z = 0
4 matrix4 = RLPy.RMatrix4( RLPy.EEulerOrder_XYZ, euler_angle_x, euler_angle_y, euler_angle_z )

__init__ ( self, rkRotate )

The constructor. Initialize a new RMatrix4 with RMatrix3.

Parameters

rkRotate [IN] Rotation 3x3 matrix - RMatrix3

Returns

Returns the row vector of the matrix - RMatrix4
1 rotate = RLPy.RMatrix3( 1, 0, 0,
2                         0, 2, 0,
3                         0, 0, 3 )
4 matrix4 = RLPy.RMatrix4( rotate )

__init__ ( self, kRotate, kTranslate, kScale )

The constructor. Initialize a new RMatrix4 with RTS.

Parameters

rkRotate [IN] Rotation matrix - RMatrix3
rkTranslate [IN] Translate vector - RVector3
rkScale [IN] Scale vector - RVector3

Returns

Returns the row vector of the matrix - RMatrix4 
1 rotate = RLPy.RMatrix3( 1, 0, 0,
2                         0, 2, 0,
3                         0, 0, 3 )
4 translate = RLPy.RVector3( 1,2,3 )
5 scale = RLPy.RVector3( 2,2,2 )
6 matrix4 = RLPy.RMatrix4( rotate, translate, scale )

__init__ ( self, args )

The constructor. Initialize a new 4x4 matrix object with another RMatrix4 object.

Parameters

args [IN] a 4x4 matrix object - RMatrix4

Returns

Returns the row vector of the matrix - RMatrix4 
1 matrix4 = RLPy.RMatrix4( 1,   2,  3,  4,
2                          5,   6,  7,  8,
3                          9,  10, 11, 12,
4                          13, 14, 15, 16 )
5 matrix4_copy = RLPy.RMatrix4( matrix4 )
6 print( matrix4_copy == matrix4 ) # true

Operators

+

The "addition" operator.

See Also: += 

 1 matrix4_a = RLPy.RMatrix4( 1, 2, 3, 4,
 2                            0, 0, 0, 0,
 3                            0, 0, 0, 0,
 4                            0, 0, 0, 0 )
 5 matrix4_b = RLPy.RMatrix4( 2, 2, 2, 2,
 6                            0, 0, 0, 0,
 7                            0, 0, 0, 0,
 8                            0, 0, 0, 0 )
 9 matrix4_result = matrix4_a + matrix4_b
10 
11 print( matrix4_result.GetRow(0)[0] == 1+2 ) # true
12 print( matrix4_result.GetRow(0)[1] == 2+2 ) # true
13 print( matrix4_result.GetRow(0)[2] == 3+2 ) # true
14 print( matrix4_result.GetRow(0)[3] == 4+2 ) # true

-

The "subtraction" operator.

See Also: -= 

 1 matrix4_a = RLPy.RMatrix4( 1, 2, 3, 4,
 2                            0, 0, 0, 0,
 3                            0, 0, 0, 0,
 4                            0, 0, 0, 0 )
 5 matrix4_b = RLPy.RMatrix4( 2, 2, 2, 2,
 6                            0, 0, 0, 0,
 7                            0, 0, 0, 0,
 8                            0, 0, 0, 0 )
 9 matrix4_result = matrix4_a - matrix4_b
10 
11 print( matrix4_result.GetRow(0)[0] == 1-2 ) # true
12 print( matrix4_result.GetRow(0)[1] == 2-2 ) # true
13 print( matrix4_result.GetRow(0)[2] == 3-2 ) # true
14 print( matrix4_result.GetRow(0)[3] == 4-2 ) # true

*

The "multiplication" operator.

See Also: *= 

 1 matrix4_a = RLPy.RMatrix4( 1, 2, 3, 4,
 2                            0, 0, 0, 0,
 3                            0, 0, 0, 0,
 4                            0, 0, 0, 0 )
 5 matrix4_b = RLPy.RMatrix4( 2, 0, 0, 0,
 6                            2, 0, 0, 0,
 7                            2, 0, 0, 0,
 8                            2, 0, 0, 0 )
 9 matrix4_result = matrix4_a * matrix4_b
10 
11 print( matrix4_result.GetRow(0)[0] == 1*2 + 2*2 + 3*2 + 4*2  ) # true

/

The "division" operator.

See Also: /= 

 1 matrix4_a = RLPy.RMatrix4( 1, 2, 3, 4,
 2                            0, 0, 0, 0,
 3                            0, 0, 0, 0,
 4                            0, 0, 0, 0 )
 5 matrix4_result = matrix4_a / 2
 6 
 7 print( matrix4_result.GetRow(0)[0] == 1/2 ) # true
 8 print( matrix4_result.GetRow(0)[1] == 2/2 ) # true
 9 print( matrix4_result.GetRow(0)[2] == 3/2 ) # true
10 print( matrix4_result.GetRow(0)[3] == 4/2 ) # true

-

The "unary minus" . 

 1 matrix4_a = RLPy.RMatrix4( 1, 2, 3, 4,
 2                            0, 0, 0, 0,
 3                            0, 0, 0, 0,
 4                            0, 0, 0, 0 )
 5 matrix4_result = -matrix4_a
 6 
 7 print( matrix4_result.GetRow(0)[0] == -1 ) # true
 8 print( matrix4_result.GetRow(0)[1] == -2 ) # true
 9 print( matrix4_result.GetRow(0)[2] == -3 ) # true
10 print( matrix4_result.GetRow(0)[3] == -4 ) # true

==

The "equal to" operator. Performs a one-by-one comparison of the matrix array.

See Also: != 

 1 matrix4_a = RLPy.RMatrix4( 1, 2, 3, 4,
 2                            0, 0, 0, 0,
 3                            0, 0, 0, 0,
 4                            0, 0, 0, 0 )
 5 matrix4_b = RLPy.RMatrix4( 1, 2, 3, 4,
 6                            0, 0, 0, 0,
 7                            0, 0, 0, 0,
 8                            0, 0, 0, 0 )
 9 
10 print( matrix4_a == matrix4_b ) # true

!=

The "not equal to" operator. Performs a one-by-one comparison of the matrix array.

See Also: == 

 1 matrix4_a = RLPy.RMatrix4( 1, 2, 3, 4,
 2                            0, 0, 0, 0,
 3                            0, 0, 0, 0,
 4                            0, 0, 0, 0 )
 5 matrix4_b = RLPy.RMatrix4( 2, 2, 2, 2,
 6                            0, 0, 0, 0,
 7                            0, 0, 0, 0,
 8                            0, 0, 0, 0 )
 9 
10 print( matrix4_a != matrix4_b ) # true

>

The "greater than" operator. Performs a one-by-one comparison of the matrix array.

See Also: >= 

 1 matrix4_a = RLPy.RMatrix4( 1, 0, 0, 0,
 2                            0, 0, 0, 0,
 3                            0, 0, 0, 0,
 4                            0, 0, 0, 0 )
 5 matrix4_b = RLPy.RMatrix4( 2, 0, 0, 0,
 6                            0, 0, 0, 0,
 7                            0, 0, 0, 0,
 8                            0, 0, 0, 0 )
 9 
10 print( matrix4_b > matrix4_a ) # true

>=

The "greater than or equal to" operator. Performs a one-by-one comparison of the matrix array.

See Also: > 

 1 matrix4_a = RLPy.RMatrix4( 1, 1, 1, 4,
 2                            0, 0, 0, 0,
 3                            0, 0, 0, 0,
 4                            0, 0, 0, 0 )
 5 matrix4_b = RLPy.RMatrix4( 1, 1, 1, 8,
 6                            0, 0, 0, 0,
 7                            0, 0, 0, 0,
 8                            0, 0, 0, 0 )
 9 
10 print( matrix4_b >= matrix4_a ) # true

<

The "less than" operator. Performs a one-by-one comparison of the matrix array.

See Also: <= 

 1 matrix4_a = RLPy.RMatrix4( 2, 0, 0, 0,
 2                            0, 0, 0, 0,
 3                            0, 0, 0, 0,
 4                            0, 0, 0, 0 )
 5 matrix4_b = RLPy.RMatrix4( 3, 0, 0, 0,
 6                            0, 0, 0, 0,
 7                            0, 0, 0, 0,
 8                            0, 0, 0, 0 )
 9 
10 print( matrix4_a < matrix4_b ) # true

<=

The "less than" operator. Performs a one-by-one comparison of the matrix array.

See Also: < 

 1 matrix4_a = RLPy.RMatrix4( 2, 2, 1, 0,
 2                            0, 0, 0, 0,
 3                            0, 0, 0, 0,
 4                            0, 0, 0, 0 )
 5 matrix4_b = RLPy.RMatrix4( 2, 2, 5, 0,
 6                            0, 0, 0, 0,
 7                            0, 0, 0, 0,
 8                            0, 0, 0, 0 )
 9 
10 print( matrix4_a <= matrix4_b ) # true

+=

The "addition assignment" operator.

See Also: + 

 1 matrix4 =  RLPy.RMatrix4( 1, 2, 3, 4,
 2                           0, 0, 0, 0,
 3                           0, 0, 0, 0, 
 4                           0, 0, 0, 0 )
 5 matrix4 += RLPy.RMatrix4( 2, 2, 2, 2,
 6                           0, 0, 0, 0,
 7                           0, 0, 0, 0,
 8                           0, 0, 0, 0 )
 9 
10 print( matrix4.GetRow(0)[0] == 1+2 ) # true
11 print( matrix4.GetRow(0)[1] == 2+2 ) # true
12 print( matrix4.GetRow(0)[2] == 3+2 ) # true
13 print( matrix4.GetRow(0)[3] == 4+2 ) # true

-=

The "subtraction assignment" operator.

See Also: - 

 1 matrix4 =  RLPy.RMatrix4( 1, 2, 3, 4,
 2                           0, 0, 0, 0,
 3                           0, 0, 0, 0,
 4                           0, 0, 0, 0 )
 5 matrix4 -= RLPy.RMatrix4( 2, 2, 2, 2,
 6                           0, 0, 0, 0,
 7                           0, 0, 0, 0,
 8                           0, 0, 0, 0 )
 9 
10 print( matrix4.GetRow(0)[0] == 1-2 ) # true
11 print( matrix4.GetRow(0)[1] == 2-2 ) # true
12 print( matrix4.GetRow(0)[2] == 3-2 ) # true
13 print( matrix4.GetRow(0)[3] == 4-2 ) # true

*=

The "multiplication assignment" operator. For the calculation method, refer to the * operator.

See Also: * 

 1 matrix4 = RLPy.RMatrix4( 1, 2, 3, 4,
 2                          0, 0, 0, 0,
 3                          0, 0, 0, 0,
 4                          0, 0, 0, 0 )
 5 matrix4 *= 2
 6 
 7 print( matrix4.GetRow(0)[0] == 1*2 ) # true
 8 print( matrix4.GetRow(0)[1] == 2*2 ) # true
 9 print( matrix4.GetRow(0)[2] == 3*2 ) # true
10 print( matrix4.GetRow(0)[3] == 4*2 ) # true

/=

The "division assignment" operator. For the calculation method, refer to the / operator.

See Also: / 

 1 matrix4 = RLPy.RMatrix4( 1, 2, 3, 4,
 2                          0, 0, 0, 0,
 3                          0, 0, 0, 0,
 4                          0, 0, 0, 0 )
 5 matrix4 /= 2
 6 
 7 print( matrix4.GetRow(0)[0] == 1/2 ) # true
 8 print( matrix4.GetRow(0)[1] == 2/2 ) # true
 9 print( matrix4.GetRow(0)[2] == 3/2 ) # true
10 print( matrix4.GetRow(0)[3] == 4/2 ) # true

Member Functions

MakeIdentity (self)

This function can be used to initialize the 3x3 matrix. It is equivalent to setting the matrix to: 

[1  0  0  0]
[0  1  0  0]
[0  0  1  0]
[0  0  0  1]

Returns

This object - RMatrix4
1 matrix4 = RLPy.RMatrix4()
2 matrix4.MakeIdentity()

M (self, args)

Get the value of an element in a 4x4 matrix by row and column index.

Parameters

nRow [IN] Index of the row in the matrix - int
nCol [IN] Index of the column in the matrix - int

Returns

The matrix element specified by row and col - float
1 matrix4 = RLPy.RMatrix4()
2 matrix4.MakeIdentity()
3 
4 print(matrix4.M(0,0)) #

E (self, args)

Get the value of an element in a 3x3 matrix by index number (from 0 to 15);

Parameters

nRow [IN] Index of the matrix.

Returns

The matrix element specified by index - float
1 matrix4 = RLPy.RMatrix4()
2 matrix4.MakeIdentity()
3 
4 print(matrix4.E(0)) #

GetRow (self, nR)

Retreive a row inside a 4x4 matrix.

Parameters

nRow [IN] Index of the row in the matrix.

Returns

The row vector of the matrix - RVector4
1 matrix4 = RLPy.RMatrix4()
2 matrix4.MakeIdentity()
3 row0 = matrix4.GetRow(0)
4 
5 print(row0[0])
6 print(row0[1])
7 print(row0[2])
8 print(row0[3])

GetColumn (self, nC)

Retrieve a column inside a 4x4 matrix.

Parameters

nRow [IN] Index of the column in the matrix.

Returns

The column vector of the matrix - RVector4
1 matrix4 = RLPy.RMatrix4()
2 matrix4.MakeIdentity()
3 col0 = matrix4.GetColumn(0)
4 
5 print(col0[0])
6 print(col0[1])
7 print(col0[2])
8 print(col0[3])

Transpose (self)

Obtain the transposed matrix by transposing the current m * n matrix into an n * m matrix by row-column swapping.

Returns

A new matrix containing this matrix's transpose - RMatrix4
 1 matrix4_orgin = RLPy.RMatrix4(  1,  2,  3,  4,
 2                                 5,  6,  7,  8,
 3                                 9, 10, 11, 12,
 4                                13, 14, 15, 16 )
 5 matrix4_transpose = matrix4_orgin.Transpose()
 6 row0 = matrix4_orgin.GetRow(0)
 7 col0 = matrix4_transpose.GetColumn(0)
 8 
 9 print(row0[0] == col0[0])
10 print(row0[1] == col0[1])
11 print(row0[2] == col0[2])
12 print(row0[3] == col0[3])

TransposeTimes (self, mM)

Multiply a transposed version of a 4x4 matrix with itself.

Parameters

mM [IN] the matrix - RMatrix4

Returns

A new matrix. (this^T * mM) - RMatrix4
 1 matrix4_orgin = RLPy.RMatrix4(  1,  2,  3,  4,
 2                                 5,  6,  7,  8,
 3                                 9, 10, 11, 12,
 4                                13, 14, 15, 16 )
 5 matrix4_transpose_value = RLPy.RMatrix4( 2, 0, 0, 0,
 6                                          0, 2, 0, 0,
 7                                          0, 0, 2, 0,
 8                                          0, 0, 0, 2 )
 9 matrix4_transpose_times = matrix4_orgin.TransposeTimes(matrix4_transpose_value)
10 row0 = matrix4_orgin.GetRow(0)
11 col0 = matrix4_transpose_times.GetColumn(0)
12 
13 print(row0[0]*2 == col0[0])
14 print(row0[1]*2 == col0[1])
15 print(row0[2]*2 == col0[2])
16 print(row0[3]*2 == col0[3])

TimesTranspose (self, mM)

Multiply this 4x4 matrix with a transposed version of itself.

Parameters

mM [IN] the matrix - RMatrix4

Returns

A new matrix. (this * M^T) - RMatrix4
 1 matrix4_orgin = RLPy.RMatrix4(  1,  2,  3,  4,
 2                                 5,  6,  7,  8,
 3                                 9, 10, 11, 12,
 4                                13, 14, 15, 16 )
 5 matrix4_transpose_value = RLPy.RMatrix4( 3, 0, 0, 0,
 6                                          0, 3, 0, 0,
 7                                          0, 0, 3, 0,
 8                                          0, 0, 0, 3 )
 9 matrix4_times_transpose = matrix4_orgin.TimesTranspose(matrix4_transpose_value)
10 row0 = matrix4_orgin.GetColumn(0)
11 col0 = matrix4_times_transpose.GetColumn(0)
12 
13 print(row0[0]*3 == col0[0])
14 print(row0[1]*3 == col0[1])
15 print(row0[2]*3 == col0[2])
16 print(row0[3]*3 == col0[3])

Inverse (self)

Obtain the inverse (reciprocal) of this 4x4 matrix (A^-1).

Returns

A new matrix containing this matrix's inverse - RMatrix4
 1 matrix4_value = RLPy.RMatrix4( 1, 2, 1, 1,
 2                                1, 1,-1,-2,
 3                                1,-1,-1, 2,
 4                                1,-2, 1,-1 )
 5 matrix4_inverse = matrix4_value.Inverse()
 6 row0_inverse = matrix4_inverse.GetRow(0)
 7 
 8 print(row0_inverse[0])
 9 print(row0_inverse[1])
10 print(row0_inverse[2])
11 print(row0_inverse[3])

Adjoint (self)

Adjugate this 4x4 matrix.

Returns

A new matrix containing this matrix's adjoint - RMatrix4
 1 matrix4_value = RLPy.RMatrix4( 1, 2, 1, 1,
 2                                1, 1,-1,-2,
 3                                1,-1,-1, 2,
 4                                1,-2, 1,-1 )
 5 matrix4_Adjoint = matrix4_value.Adjoint()
 6 row0_Adjoint = matrix4_Adjoint.GetRow(0)
 7 
 8 print(row0_Adjoint[0])
 9 print(row0_Adjoint[1])
10 print(row0_Adjoint[2])
11 print(row0_Adjoint[3])

AdjointTranspose (self)

Adjugate and transpose this 4x4 matrix.

Returns

A new matrix - RMatrix4
 1 matrix4_value = RLPy.RMatrix4( 1, 2, 1, 1,
 2                                1, 1,-1,-2,
 3                                1,-1,-1, 2,
 4                                1,-2, 1,-1 )
 5 matrix4_Adjoint_transpose = matrix4_value.AdjointTranspose()
 6 col0_Adjoint_transpose = matrix4_Adjoint_transpose.GetColumn(0)
 7 
 8 print(col0_Adjoint_transpose[0] == row0_Adjoint[0])
 9 print(col0_Adjoint_transpose[1] == row0_Adjoint[1])
10 print(col0_Adjoint_transpose[2] == row0_Adjoint[2])
11 print(col0_Adjoint_transpose[3] == row0_Adjoint[3])

InverseTranspose (self)

Invert and transpose this 4x4 matrix.

Returns

A new matrix - RMatrix4
 1 matrix4_value = RLPy.RMatrix4( 1, 2, 1, 1,
 2                                1, 1,-1,-2,
 3                                1,-1,-1, 2,
 4                                1,-2, 1,-1 )
 5 matrix4_inverse_transpose = matrix4_value.InverseTranspose()
 6 col0_inverse_transpose = matrix4_inverse_transpose.GetColumn(0)
 7 
 8 print(col0_inverse_transpose[0] == row0_inverse[0])
 9 print(col0_inverse_transpose[1] == row0_inverse[1])
10 print(col0_inverse_transpose[2] == row0_inverse[2])
11 print(col0_inverse_transpose[3] == row0_inverse[3])

Determinant (self)

Obtain the scalar value for this 4x4 matrix (|A|).

Rlpy rmatrix4 determinant.jpg

Returns

The determinant of the matrix - float
1 matrix4_value = RLPy.RMatrix4( 1, 2, 1, 1,
2                                1, 1,-1,-2,
3                                1,-1,-1, 2,
4                                1,-2, 1,-1 )
5 print(matrix4_value.Determinant())

MaxColumn (self)

Find the maximum absolute value within this 4x4 matrix, and return the column in which the value is located. If all of the elements within the 4x4 matrix are 0 then return -1.

Returns

Return index of column of M containing maximum abs entry, or -1 if M = 0 - int
1 matrix4_column_value = RLPy.RMatrix4( 1, 2, 3,-5,
2                                       0, 0, 0, 0,
3                                       0, 0, 0, 0,
4                                       0, 0, 0, 0 )
5 print(matrix4_column_value.MaxColumn()) # column:3 -> abs(-5)

MaxRow (self)

Find the maximum absolute value within this 4x4 matrix, and return the row in which the value is located. If all of the elements within the 4x4 matrix are 0 then return -1.

Returns

Return index of row of M containing maximum abs entry, or -1 if M = 0 - int
1 matrix4_row_value = RLPy.RMatrix4( 1, 0, 0, 0,
2                                    2, 0, 0, 0,
3                                    3, 0, 0, 0,
4                                   -5, 0, 0, 0 )
5 print(matrix4_value.MaxRow()) # Row:3 -> abs(-5)

OneNorm (self)

Return the sum of the column elements that contain the largest absolute values.

Returns

Return Norm - float
1 matrix4_row_value = RLPy.RMatrix4( 1, 0, 0, 0,
2                                    2, 0, 0, 0,
3                                    3, 0, 0, 0,
4                                   -5, 0, 0, 0 )
5 print(matrix4_row_value.OneNorm()) # 11 -> 1+2+abs(-5)

InfNorm (self)

Return the sum of the row elements that contain the largest absolute values.

Returns

Return InfNorm - float
1 matrix4_column_value = RLPy.RMatrix4( 1, 2, 3,-5,
2                                       0, 0, 0, 0,
3                                       0, 0, 0, 0,
4                                       0, 0, 0, 0 )
5 print(matrix4_column_value.InfNorm()) # 11 -> 1+2+abs(-5)

FromRTS (self, kRotate, kTranslate, kScale)

Apply rotate, translate, and scale data to a 4x4 matrix.

Parameters

kRotate [IN] Rotate Matrix - RMatrix3
kTranslate [IN] Translate vector - RVector3
kScale [IN] Scale vector - RVector3

Returns

Return a new matrix from RTS - RMatrix4
 1 rotate = RLPy.RMatrix3( 1, 0, 0,
 2                         0, 1, 0,
 3                         0, 0, 1 )
 4 translate = RLPy.RVector3( 1, 0, 0 )
 5 scale = RLPy.RVector3( 2, 2, 2 )
 6 matrix4_result =  RLPy.RMatrix4().FromRTS( rotate, translate, scale )
 7 row0 = matrix4_result.GetRow(0)
 8 
 9 print(row0[0])
10 print(row0[1])
11 print(row0[2])
12 print(row0[3])

GetSimpleRTS (self, rkRotate, rkTranslate, rkScale)

Retrieve rotation, translation, and scale data from this 4x4 matrix.

Parameters

rkRotate [IN] Angle of x-axis in radians - float
rkTranslate [IN] Angle of y-axis in radians - float
rkScale [IN] Angle of z-axis in radians - float

Returns

 1 matrix4_value = RLPy.RMatrix4( 1, 2, 1, 1,
 2                                1, 1,-1,-2,
 3                                1,-1,-1, 2,
 4                                1,-2, 1,-1 )
 5 rotate = RLPy.RMatrix3()
 6 translate = RLPy.RVector3()
 7 scale = RLPy.RVector3()
 8 matrix4_value.GetSimpleRTS( rotate, translate, scale )
 9 row0 = rotate.GetRow(0)
10 
11 print(row0[0])
12 print(row0[1])
13 print(row0[2])
14 
15 print(translate[0])
16 print(translate[1])
17 print(translate[2])
18 
19 print(scale[0])
20 print(scale[1])
21 print(scale[2])

GetSimpleRotate (self, rkRotate)

Retrieve rotation data from this 4x4 matrix.

Parameters

rkRotate [IN] Rotation Matrix - RMatrix3

Returns

3x3 matrix rotation data of this 4x4 matrix.
 1 matrix4_value = RLPy.RMatrix4( 1, 2, 1, 1,
 2                                1, 1,-1,-2,
 3                                1,-1,-1, 2,
 4                                1,-2, 1,-1 
 5 rotate = RLPy.RMatrix3()
 6 matrix4_value.GetSimpleRotate( rotate )
 7 row0 = rotate.GetRow(0)
 8 
 9 print(row0[0])
10 print(row0[1])
11 print(row0[2])

SetTranslateZero (self)

Set the translation data in this 4x4 matrix to 0. 

 1 matrix4_value = RLPy.RMatrix4( 1, 2, 1, 1,
 2                                1, 1,-1,-2,
 3                                1,-1,-1, 2,
 4                                1,-2, 1,-1 
 5 matrix4_value.SetTranslateZero()
 6 row3 = matrix4_value.GetRow(3)
 7 
 8 print(row3[0] == 0)
 9 print(row3[1] == 0)
10 print(row3[2] == 0)

RotationX (self, fAngle)

Rotation matrix for rotations around x-axis.

Parameters

fAngle [IN] angle in radians - float

Returns

Return a new matrix of for rotations around x-axis - RMatrix4
1 matrix4_orgin = RLPy.RMatrix4()
2 matrix4_orgin.MakeIdentity()
3 matrix4_orgin.RotationX( 90 * RLPy.RMath.CONST_DEG_TO_RAD )

RotationY (self, fAngle)

Rotation matrix for rotations around y-axis.

Parameters

fAngle [IN] angle in radians - float

Returns

Return a new matrix of for rotations around y-axis - RMatrix4
1 matrix4_orgin = RLPy.RMatrix4()
2 matrix4_orgin.MakeIdentity()
3 matrix4_orgin.RotationY( 90 * RLPy.RMath.CONST_DEG_TO_RAD )

RotationZ (self, fAngle)

Rotation matrix for rotations around z-axis.

Parameters

fAngle [IN] angle in radians - float

Returns

Return a new matrix of for rotations around z-axis - RMatrix4
1 matrix4_orgin = RLPy.RMatrix4()
2 matrix4_orgin.MakeIdentity()
3 matrix4_orgin.RotationZ( 90 * RLPy.RMath.CONST_DEG_TO_RAD )

RotateAxisAngle (self, rkAxis, fAngle)

Rotation matrix from axis angle.

Parameters

rkAxis [IN] axis vector - RVector3
fAngle [IN] angle in radians - float

Returns

Return a new matrix from specified axis angle - RMatrix4
 1 matrix4_value = RLPy.RMatrix4( 1, 2, 1, 1,
 2                                1, 1,-1,-2,
 3                                1,-1,-1, 2,
 4                                1,-2, 1,-1 
 5 x_axis_vector = RLPy.RVector3( 1, 0, 0 )  # axis = "X"
 6 y_axis_vector = RLPy.RVector3( 0, 1, 0 )  # axis = "Y"
 7 z_axis_vector = RLPy.RVector3( 0, 0, 1 )  # axis = "Z"    
 8 matrix4_value.RotateAxisAngle( x_axis_vector, 90 * RLPy.RMath.CONST_DEG_TO_RAD )
 9 matrix4_value.RotateAxisAngle( y_axis_vector, 90 * RLPy.RMath.CONST_DEG_TO_RAD )
10 matrix4_value.RotateAxisAngle( z_axis_vector, 90 * RLPy.RMath.CONST_DEG_TO_RAD )

FromEulerAngle (self, Oreder, rx, ry, rz)

Convert Euler angle to a 4x4 matrix according to a rotation axis order.

Parameters

Oreder [IN] Euler order - RLPY.EEulerOrder
  • EEulerOrder_XYZ = _RLPy.EEulerOrder_XYZ
  • EEulerOrder_ZYX = _RLPy.EEulerOrder_ZYX
  • EEulerOrder_XZY = _RLPy.EEulerOrder_XZY
  • EEulerOrder_YZX = _RLPy.EEulerOrder_YZX
  • EEulerOrder_YXZ = _RLPy.EEulerOrder_YXZ
  • EEulerOrder_ZXY = _RLPy.EEulerOrder_ZXY
rx [IN] Angle of x-axis in radians - float
ry [IN] Angle of y-axis in radians - float
rz [IN] Angle of z-axis in radians - float

Returns

Return a new matrix from specified axis angle - RMatrix4
 1 euler_angle_x = 90 * RLPy.RMath.CONST_DEG_TO_RAD
 2 euler_angle_y = 0
 3 euler_angle_z = 0
 4 matrix4_result = RLPy.RMatrix4().FromEulerAngle( RLPy.EEulerOrder_XYZ, euler_angle_x, euler_angle_y, euler_angle_z)
 5 row0 = matrix4_result[0].GetRow(0)
 6 
 7 print(row0[0])
 8 print(row0[1])
 9 print(row0[2])
10 print(row0[3])

SetSR (self, mSR)

Set scale and rotation part of the matrix.

Parameters

mSR [IN] 3x3 matrix - RMatrix3

Returns

Return a new 4x4 matrix - RMatrix4
1 matrix4_orgin = RLPy.RMatrix4()
2 matrix4_orgin.MakeIdentity()
3 matrix3_rotate_value = RLPy.RMatrix3( 1, 0, 0,
4                                       0, 1, 0,
5                                       0, 0, 1 )
6 matrix4_orgin.SetSR(matrix3_rotate_value)

GetSR (self)

Get scale and rotation part of the matrix.

Returns

Return a 3x3 matrix - RMatrix3
1 matrix4_value = RLPy.RMatrix4( 1, 2, 1, 1,
2                                1, 1,-1,-2,
3                                1,-1,-1, 2,
4                                1,-2, 1,-1 
5 result = matrix4_value.GetSR()
6 row0 = result.GetRow(0)
7 print(row0[0])
8 print(row0[1])
9 print(row0[2])

SetTranslate (self, vTranslate)

Set translate of the matrix.

Parameters

vTranslate [IN] Translate vector - RVector3

Returns

New matrix with the specified translation - RMatrix4
1 matrix4_orgin = RLPy.RMatrix4()
2 matrix4_orgin.MakeIdentity()
3 matrix4_orgin.SetTranslate(RLPy.RVector3( 1, 2, 3 ) )

GetTranslate (self)

Get translate of the matrix.

Returns

Return a translate vector - RVector3
1 matrix4_orgin = RLPy.RMatrix4()
2 matrix4_orgin.MakeIdentity()
3 matrix4_orgin.SetTranslate(RLPy.RVector3( 1, 2, 3 ) )
4 result = matrix4_orgin.GetTranslate()
5 
6 print(result[0] == 1)
7 print(result[1] == 2)
8 print(result[2] == 3)

AccuScale (self, rkScale)

Accumulate this 4x4 matrix with scale vector.

Parameters

rkScale [IN] Scale vector - RVector3

Returns

Accumulate of this 4x4 matrix with scale vector - RMatrix4
 1 matrix4_orgin = RLPy.RMatrix4()
 2 matrix4_orgin.MakeIdentity()
 3 matrix4_orgin.AccuScale(RLPy.RVector3( 2, 2, 2 ) )
 4 matrix4_orgin.AccuScale(RLPy.RVector3( 3, 3, 3 ) )
 5 result = matrix4_orgin.GetSR()
 6 row0 = result.GetRow(0)
 7 print(row0[0] == 2*3)
 8 row1 = result.GetRow(1)
 9 print(row1[1] == 2*3)
10 row2 = result.GetRow(2)
11 print(row2[2] == 2*3)

AccuRotate (self, rkRotate)

Accumulate this 4x4 matrix with rotation matrix.

Parameters

rkRotate [IN] Rotation matrix - RMatrix3

Returns

Accumulate this 4x4 matrix and rotation matrix - RMatrix4
 1 matrix4_orgin = RLPy.RMatrix4()
 2 matrix4_orgin.MakeIdentity()
 3 matrix3_orgin = RLPy.RMatrix3()
 4 matrix3_orgin.FromAxisAngle( RLPy.RVector3( 0, 1, 0 ), 90 * RLPy.RMath.CONST_DEG_TO_RAD )
 5 matrix4_orgin.AccuRotate(matrix3_orgin)
 6 matrix4_orgin.AccuRotate(matrix3_orgin)
 7 rotate = RLPy.RMatrix3()
 8 matrix4_orgin.GetSimpleRotate( rotate )
 9 row0 = rotate.GetRow(0)
10 print(row0[0])
11 print(row0[1])
12 print(row0[2])

AccuTranslate (self, rkTranslate)

Accumulate this 4x4 matrix with translate vector.

Parameters

rkTranslate [IN] Translate vector - RVector3

Returns

Accumulate of this 4x4 matrix and translation vector - RMatrix4
1 matrix4_orgin = RLPy.RMatrix4()
2 matrix4_orgin.MakeIdentity()
3 matrix4_orgin.AccuTranslate(RLPy.RVector3( 1, 2, 3 ) )
4 matrix4_orgin.AccuTranslate(RLPy.RVector3( 2, 2, 2 ) )
5 row3 = matrix4_orgin.GetRow(3)
6 print(row3[0] == 1+2)
7 print(row3[1] == 2+2)
8 print(row3[2] == 2+3)
Retrieved from "http://wiki.reallusion.com/index.php?title=IC_Python_API:RLPy_RMatrix4&oldid=4534"